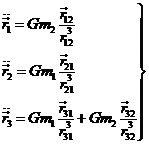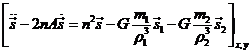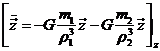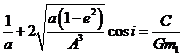7.5 Problema de los tres cuerpos
Llamaremos problema de los tres
cuerpos al caso particular del de los n-cuerpos para n = 3.
El sistema (1.7)
en el caso newtoniano se escribirá:
(38.7)
y equivaldrá a un sistema
de nueve ecuaciones escalares diferenciales de segundo orden. El orden del
sistema será, por tanto, 18, lo cual quiere decir que se precisarán 18
constantes de integración para que quede completamente determinado el
movimiento de los tres cuerpos.
De la misma manera que en 7.2 se pueden obtener también aquí diez integrales primeras:
las seis del momento lineal
(39.7)
(40.7)
las tres del momento
angular
(41.7)
y la de la
energía
(42.7)
donde T
y U tienen
el mismo significado
que (2.7) y (3.7) para i = 1,2,3 y
.
Conocidas estas integrales el orden
del sistema puede reducirse a 18 — 10 = 8. También se consigue una reducción de
dos órdenes más aplicando lo que se llama la eliminación de los nodos,
que consiste en eliminar la variable tiempo y elegir como una de las
coordenadas de posición del sistema el ángulo formado por la normal al plano de
los tres cuerpos y un eje fijo. Esta reducción, que ya estaba implícitamente
contenida en los trabajos de Lagrange, fue desarrollada por primera vez con
toda precisión por Jacobi en 1842.
Sundman en 1912 obtuvo una
solución general del problema de los tres cuerpos; pero, su expresión es tan
complicada y las series utilizadas tan lentamente convergentes que la hacen
impracticable. Las únicas integrales primeras con las que se puede contar, por
el momento, son las diez mencionadas, llamadas integrales clásicas. Sin
embargo, existen, como veremos, situaciones especiales en que el problema se
puede resolver analíticamente.
7.5.1 Caso en que r12
« r13 y r12 « r23
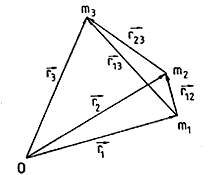
Supongamos tres cuerpos de masa m1,
m2, m3 y sean (Fig.
2.7) 
y 
. Sería, por ejemplo, el caso de la Tierra (m1),
la Luna (m3) y un satélite artificial de la Tierra (m2).
Para simplificar haremos:
, 
, 
FIG. 2.7
Sustituyendo en las dos primeras
ecuaciones del sistema (38.7) explicitando el valor de G,
tendremos:
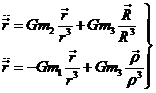(43.7)
y restando miembro a
miembro:
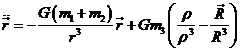
o también, haciendo G(m1 + m2)
= μ
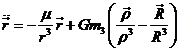(44.7)
que expresa el movimiento del satélite artificial
alrededor de la Tierra perturbado por la presencia de la Luna. El segundo
término del segundo miembro es la fuerza perturbatriz 
que interesa expresar
en función de 
y 
para estudios
posteriores.
FIG.3.7
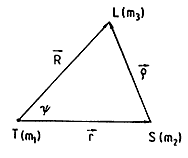
Del triángulo de la Fig.
3.7 deducimos:
(45.7)
(46.7)
o también:
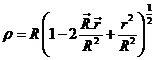
de donde:
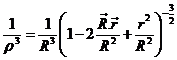
y teniendo en cuenta que r « R y
por tanto 
:
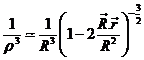
que desarrollado en serie
da
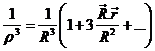
Con todo ello y teniendo en cuenta (45.7), f será:
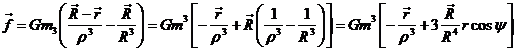
y si r 
R
todavía
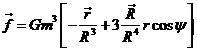
Esta
fórmula, ya de por sí muy sencilla, se puede simplificar todavía más si se
considera que durante una revolución del satélite en torno a la Tierra, la Luna
se desplaza menos de 1º y por tanto se puede tomar constante en una
vuelta.
7.5.2 El problema restringido circular
En este caso se supone despreciable la masa de uno de los cuerpos, por ejemplo
la masa m3, respecto a las masas m1 y m2
de los otros dos cuerpos, de modo que m1 y m2
perturban el movimiento del cuerpo de masa m3
pero m3
no influye
en el movimiento de los cuerpos de masas m1 y m2.
Supondremos m1 > m2
y que la órbita relativa de m2 respecto a m1 es una circunferencia. Se
tratará pues de estudiar el movimiento de tres cuerpos de los cuales dos de
masa finita giran uno alrededor del otro en órbitas circulares mientras un
tercer cuerpo de masa infinitesimal se mueve en su campo. Esta situación que
fue estudiada principalmente por Poincaré y Hill entre otros, se halla con
alguna aproximación en el Sistema Solar.
Tomemos el
sistema (38.7) y escribámoslo para este caso:
(47.7)
Restando las dos primeras ecuaciones
y haciendo 
resulta:
(48.7)
con μ = G (m1+ m2).
La ecuación (48.7)
expresa el movimiento relativo del cuerpo de masa m2 con
respecto al de masa ml. La tercera ecuación de (47.7) nos da el movimiento del tercer cuerpo de masa m3.
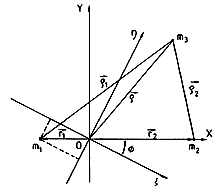
Supongamos que O es el centro de gravedad de los
cuerpos de masas ml y m2 (Fig. 4.7). Puesto que m3 es infinitamente
pequeña se puede suponer que O es también el centro de gravedad de los tres
cuerpos.
FIG. 4.7
Tomemos dos sistemas de coordenadas con origen en O definidos: uno de
ellos, x, y, z, móvil, de modo que el eje x coincida con la recta
que une los cuerpos de masas m1 y m2,
el eje y esté situado en el plano de la órbita que describe el cuerpo de
masa m2 alrededor del de masa m1
y el eje z formando triedro trirrectángulo con ellos; el otro ξ, η, ζ, que no gire con los cuerpos, es decir, fijo en
el espacio y tal que ζ = z.
Para pasar de la base ξ, η, ζ, a
la base x, y, z utilizaremos la matriz
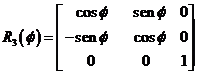(49.7)
donde
es el ángulo
que forman los ejes ξ y x en cada instante.
Estudiaremos el movimiento del cuerpo de
masa m3 respecto a los ejes móviles. Por comodidad
en la notación haremos:
con lo cual la tercera ecuación de (47.7) se escribirá:
(50.7)
Para simplificar el problema podemos
considerar un espacio más reducido (plano) y definir los vectores
y la matriz de giro
que aplicada a 
nos dará 
Con
este convenio la equivalente a la ecuación (50.7) será:
(51.7)
Recordemos
las siguientes propiedades de la matriz M():
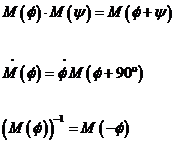
Luego,
(52.7)
y derivando dos veces:
(53.7)
(54.7)
Ahora bien, teniendo en cuenta la
definición que hemos dado de , si n es el movimiento medio del cuerpo de masa m2
y 
es un valor inicial de será
de donde
Suponiendo = 0 ,
tendremos, al sustituir en (52.7), (53.7)
y (54.7):
(55.7)
(56.7)
(57.7)
la expresión (55.7) escrita para 
y 
y
sustituida en (51.7) nos dará
y multiplicando por la izquierda por M() teniendo en cuenta el valor de 
dado por
(57.7) y que
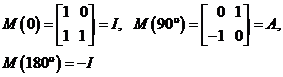
obtenemos:
(58.7)
y
como que el tercer eje es común:
(59.7)
En el sistema de ejes móviles las
coordenadas de los cuerpos de masas m1 y m2
son respectivamente (x1, 0, 0) y (x2,
0, 0); por tanto, los vectores 
y 
que figuran en (58.7) serán
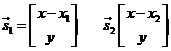
Veamos ahora cual es el significado del término 
. Recordando el significado de A y 
tenemos:
(60.7)
y considerando por otra parte el vector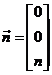 
, podemos escribir
(61.7)
Comparando, pues, (60.7)
con (61.7) vemos que
Luego, podemos escribir conjuntamente (58.7) y (59.7) en la forma
(62.7)
siendo
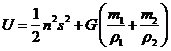
La
ecuación (62.7) se puede integrar fácilmente
multiplicando sus dos miembros escalarmente por 
:
(63.7)
pero, 
y 
por tanto, podemos escribir
(63.7) en la forma
de donde
(64.7)
expresión que recibe el
nombre de integral de Jacobi o de la energía relativa y que nos da el
módulo de la velocidad del cuerpo infinitesimal en cada posición en el sistema
móvil.
La
integral de Jacobi se puede expresar también en función de las coordenadas y
las componentes de la velocidad en el sistema de coordenadas fijo,
obteniéndose:
(65.7)
siendo
v la velocidad del cuerpo de masa m3 en
el sistema fijo.
7.5.3
Criterio de Tisserand
Una aplicación de la ecuación de
Jacobí es el criterio de Tisserand para la identificación de cometas.
Si un cometa se aproxima mucho a
Júpiter, o a otro de los planetas, su órbita puede resultar muy perturbada y, a
menos que alguna propiedad de su órbita heliocéntrica no se vea afectada por la
perturbación planetaria, en su nuevo paso será difícil identificarlo.
Tisserand consideró la situación Sol
- planeta – cometa como un ejemplo del problema restringido circular de los
tres cuerpos en que el cometa juega el papel de cuerpo de masa infinitesimal.
El planeta es generalmente Júpiter, de gran masa y distancia al Sol grande, y
cuya órbita, aunque no circular, de excentricidad suficientemente pequeña para
poderse despreciar. En la integral de Jacobi, aunque el cometa sea perturbado
por Júpiter, la constante C se conservará invariante y dicha invariancia
permitirá identificar el cometa.
Utilizaremos para sustituir en (65.7) los elementos orbitales de los dos posibles cometas
en lugar de las coordenadas y velocidad de los mismos.
En el caso de Júpiter y el Sol es 
, de modo que el centro del Sol puede tomarse como origen sin
error sensible. Si 
y 
son el radio vector
heliocéntrico del cometa y la constante de las áreas en el problema de los dos
cuerpos Sol - cometa, i, a y e son respectivamente la inclinación
de la órbita del cometa con respecto al plano de la órbita de Júpiter alrededor
del Sol, el semieje mayor y la excentricidad de la órbita del cometa, la
integral de la energía del cometa nos da
y la integral de las áreas
con
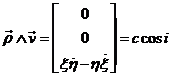
y
Sustituyendo estas expresiones en (65.7) obtenemos:
(66.7)
( 
= distancia
Júpiter-cometa).
Ahora
bien, si designamos por A la
distancia de Júpiter al Sol es
de donde,
y sustituyendo en (66.7) y operando, teniendo en cuenta que m2/m10.001, resulta, suprimiendo los términos afectados por dicho
cociente
(67.7)
Si observarnos, pues, el
paso de los que parecen ser dos cometas y los elementos orbitales que intervienen
en la fórmula (67.7) del primero son a0, e0, i0 y del segundo
a1, e1, i1 y se verifica
(68.7)
es muy probable que se trate de un mismo cometa;
pero, si los dos miembros de (68.7) son muy distintos,
podemos asegurar que se trata de dos cometas distintos. Tal es el criterio de
Tisserand válido sólo aproximadamente. Debemos observar que aun que en la
deducción de la fórmula (67.7) se ha utilizado la
inclinación de la órbita del cometa respecto a la de Júpiter, en la práctica, y
sin error notable, en la fórmula (68.7) se utiliza la
inclinación de la órbita del cometa respecto a la eclíptica.