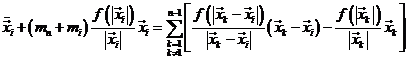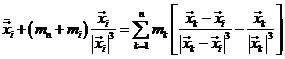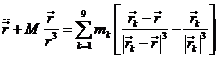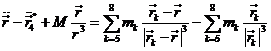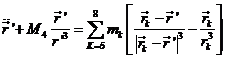7.4 Coordenadas relativas
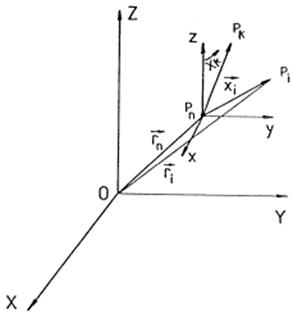
Sean n cuerpos Pi(i
= 1,2,...,n) de masas respectivas mi referidas a un sistema
de coordenadas cartesianas (O; X,Y,Z) (Fig. 1.7).
Sean 
sus posiciones.
FIG. 1.7
Tomemos el cuerpo Pn como origen
de un nuevo sistema de coordenadas x,y,z. Si designamos por 
el vector de posición del cuerpo Pi en este
nuevo sistema, será:
(28.7)
Veamos como se escribirán las ecuaciones (1.7) en este sistema
de coordenadas relativas.
Según (28.7) se tiene
(29.7)
Aislando los términos para k=n
en la primera sumación y para k=i en la segunda, resulta:
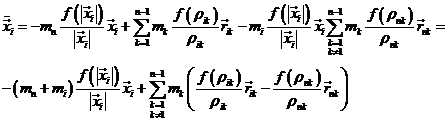
o también:
(30.7)
Haciendo
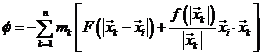
con F dada por (4.7), se comprueba que
el segundo miembro de (30.7) es el gradiente
de la función 
con respecto a .
En particular, para el caso
newtoniano es
y
Por consiguiente:
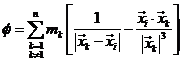
y
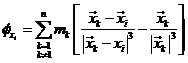(31.7)
Luego:
(32.7)
Los primeros términos del segundo miembro son las atracciones
directas sobre el cuerpo de masa mi debidas a los cuerpos perturbadores. Los
segundos términos reciben el nombre de términos (o atracciones) indirectos.
7.4.1 Aplicación al Sistema Solar
Consideremos las ecuaciones del
movimiento de un cuerpo de masa despreciable (un cometa, por ejemplo) en el
Sistema Solar. Si tomamos como origen de coordenadas relativas el Sol y
llamamos 
al vector de posición
del cometa y 
(k = 1,2,...,9)
los vectores de posición heliocéntricos de los planetas, según (32.7), tendremos:
(33.7)
donde M representa la masa del Sol, mk
las masas de cada uno de los planetas (recordemos que G = 1).
representa la sumación sobre los nueve planetas en orden de
distancias medias crecientes del planeta al Sol. Debido al movimiento propio de
los cometas el término de mayor contribución en el segundo miembro es el
relativo a Júpiter, m5, pudiendo ser los efectos de los demás
planetas relativamente pequeños. En la práctica, por consiguiente, la fórmula (33.7) se puede simplificar; pero, en cada caso, las simplificaciones deberán ser
justificadas. Así, a menos que el cometa se mueva en su órbita muy cerca de
Plutón, el término k = 9 se puede despreciar puesto que tanto las
atracciones directas como las indirectas de (33.7) son
muy pequeñas. No sucede lo mismo en el caso de Mercurio en que dichos términos
no son despreciables.
El término indirecto debido a Mercurio es:
Si llamamos 
al centro de masas del
Sol y de Mercurio, tendremos:
lo que da lugar a:
Por consiguiente, después de estas
consideraciones podemos escribir (33.7) en la forma
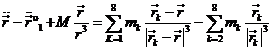(34.7)
Observamos que despreciar un
término indirecto afecta, parcialmente, a un cambio de origen del sistema de
referencia. En trabajos prácticos sobre perturbaciones cometarias conviene
muchas veces despreciar los planetas Mercurio, Venus, La Tierra y Marte debido
a la pequeñez de sus perturbaciones directas. Las perturbaciones indirectas son
absorbidas por un cambio de origen al centro de masas del Sol y los cuatro
planetas citados. Si el vector de posición de dicho centro de masas es 
escribiremos:
(35.7)
está tabulado en “Planetary coordinates for the years...”
Si el cometa es tal que |r| » |rk| (k=l,2,3,4) entonces
y haciendo
es
Por otra parte, si tomamos:
(36.7)
podemos
escribir (35.7) en la forma:
A la suma (36.7) se la
llamaba antiguamente “caída de los planetas dentro del Sol”. La fórmula (37.7) nos da el movimiento del cometa con respecto al
baricentro rº4 en función de las posiciones heliocéntricas de
los planetas Júpiter, Saturno, Urano y Neptuno.