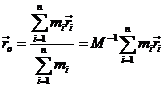7.2 Las diez integrales clásicas
Las ecuaciones (1.7) constituyen un sistema de 3n ecuaciones
escalares diferenciales de segundo orden. Por tanto, el sistema es de orden 6n
y se necesitarían para resolverlo completamente 6n constantes de
integración, es decir, 6n funciones de ![]() ,
, ![]() , t que permanecieran constantes durante el
movimiento. Se conocen si n=2; pero, en el caso general sólo se conocen
10.
, t que permanecieran constantes durante el
movimiento. Se conocen si n=2; pero, en el caso general sólo se conocen
10.
Sumando las ecuaciones (1.7),
teniendo en cuenta que ![]() , obtenemos
, obtenemos
![]() (10.7)
(10.7)
e integrando dos veces:
y
expresiones que constituyen seis integrales primeras cuyas
seis constantes de integración son las componentes de los vectores ![]() y
y ![]() .
.
Para hallar el significado de estas integrales
definamos el centro de masas de los n cuerpos
por el vector de posición ![]() :
:
con ![]() .
.
Teniendo en cuenta (1l.7),(12.7) y (13.7)
resulta:
![]() (14.7)
(14.7)
![]() (15.7)
(15.7)
relaciones que nos dicen que el centro de masas
del sistema se mueve en el espacio con movimiento rectilíneo y uniforme.
Las integrales (11.7) y (12.7) reciben el nombre de integrales
del centro de gravedad o del momento lineal.
Multiplicando vectorialmente
las ecuaciones (1.7) por ![]() y sumando se obtiene:
y sumando se obtiene:
Pero,
![]()
y
![]()
por consiguiente, en el segundo miembro de (16.7) se van destruyendo los términos dos a dos y en
consecuencia queda:
![]() (17.7)
(17.7)
e integrando, teniendo en cuenta la igualdad
![]()
se obtiene
expresión que aporta tres nuevas integrales
primeras al problema que reciben el nombre de integrales de las áreas o
del momento angular. El vector ![]() es el momento
angular y sus componentes constituyen otras tres constantes de integración.
es el momento
angular y sus componentes constituyen otras tres constantes de integración.
La ecuación (18.7)
nos dice que el momento angular de las masas en el sistema es constante. El
vector ![]() define un plano
llamado plano invariante de Laplace inclinado
1,5º respecto al plano de la eclíptica y situado entre los planos orbitales de
Júpiter y Saturno.
define un plano
llamado plano invariante de Laplace inclinado
1,5º respecto al plano de la eclíptica y situado entre los planos orbitales de
Júpiter y Saturno.
Para hallar la décima constante de integración
multipliquemos escalarmente la ecuación (6.7) por ![]() y sumemos con respecto
al índice i. Obtendremos:
y sumemos con respecto
al índice i. Obtendremos:
![]() (19.7)
(19.7)
e integrando:
o lo que es lo mismo (ver (2.7)):
expresión que constituye la llamada integral de
la energía siendo la constante de integración h la energía del
sistema.
El primer miembro de la ecuación
(21.7) es la energía cinética del sistema, mientras que -U
es la energía potencial. Por consiguiente, dicha ecuación (21.7)
establece que la energía total del sistema de los n cuerpos es constante.
Dicho de otra forma, el sistema es conservativo.
Las expresiones dadas por (11.7), (12.7), (18.7)
y (20.7) se denominan integrales clásicas del
problema de los n cuerpos. De momento no se conocen más. Bruns y Poincaré demostraron que,
aparte de las diez encontradas, no existen otras integrales del problema de los
n cuerpos que den ecuaciones que contengan sólo funciones, algebraicas o
integrales, de las coordenadas y velocidades de los cuerpos válidas para todas
las masas y que satisfagan las ecuaciones del movimiento.
Es posible reducir el orden
del problema utilizando las diez integrales clásicas; el origen de coordenadas
puede trasladarse al centro de masas del sistema y con la ayuda de las
integrales del área y de la energía se obtiene un sistema de orden (6n -
10).