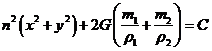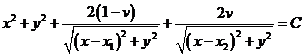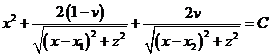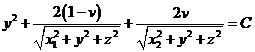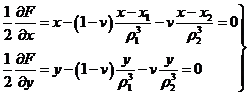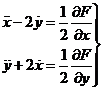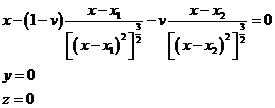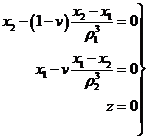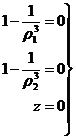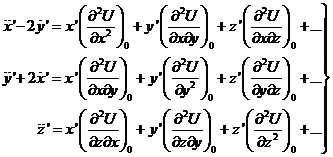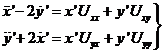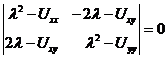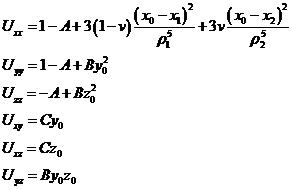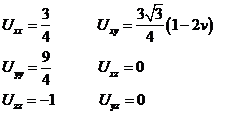7.5.4 Superficies de velocidad relativa
nula
La ecuación (64.7) es una relación entre el
cuadrado de la velocidad y las coordenadas del cuerpo infinitesimal referido a los
ejes que giran. Por consiguiente, cuando se ha determinado la constante de
integración C numéricamente, por las condiciones iniciales, dicha
ecuación determina la velocidad con que el cuerpo infinitesimal se moverá en
todos los puntos del espacio que gira; y, recíprocamente, para una velocidad
dada, la ecuación (64.7) da el lugar de puntos
del espacio relativo donde puede estar el cuerpo de masa infinitesimal.
En
particular, si en (64.7) hacemos V = 0,
nos queda
2 U= C
o teniendo en cuenta el valor de U:
Pero, recordando que G(ml + m2) = n2A3
con A=rl +r2,
podemos escribir (69.7) de la forma:
![]()
y tomando A=1, ml +m2
=1, m2/(ml+m2) = v, ml/(ml+m2)
= 1-v, finalmente:
donde
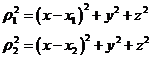
Para un
dado valor de C (70.7) será el lugar de puntos
situados en la superficie representada por la misma fórmula (70.7)
y para distintos valores de C tendremos el lugar de superficies en el
espacio definidas por (70.7).
La ecuación (70.7)
define, para un dado valor de C los límites de las regiones en que el
cuerpo de masa m3 puede moverse. Es evidente que
estas regiones son aquellas para las cuales es 2U > C pues de lo
contrario V2 sería negativo y resultarían valores
imaginarios para la velocidad. Dicha ecuación recibe el nombre de superficie
límite de Hill y no nos dice nada acerca de las órbitas que la
partícula describe en el espacio en que se puede mover. Para obtenerlas es
preciso conocer otras integrales del problema.
Las
superficies expresadas por la ecuación (70.7)
corresponden a las superficies de potencial constante ya que 2U = C.
Puesto que en (70.7) y y z figuran sólo elevadas al cuadrado, resulta
que las superficies límites de Hill son simétricas respecto al plano xy
y respecto al plano xz, y cuando v = 1/2 también con respecto al
plano yz (si v = 1/2 los puntos x1 y
x2 están situados simétricamente respecto al
origen). Las superficies para ![]() pueden considerarse
como deformaciones de
aquellas para las cuales v = 1/2.
pueden considerarse
como deformaciones de
aquellas para las cuales v = 1/2.
Para tener una idea aproximada de la forma de estas superficies
estudiaremos la de las curvas que resultan al cortar por los planos de
referencia.
La ecuación
de las curvas de intersección de las superficies con el plano xy se
obtiene haciendo z = 0 en (70.7) y de la fórmula
es
Para
valores muy grandes de x y de y que satisfagan esta ecuación, el
tercer y cuarto términos no son demasiado importantes y la ecuación puede
escribirse
![]()
donde ![]() es una cantidad pequeña. Esta ecuación representa un círculo
de radio
es una cantidad pequeña. Esta ecuación representa un círculo
de radio ![]() ; por consiguiente, una rama de la curva en el plano xy
es aproximadamente un óvalo circular asintótico al cilindro de eje el eje z
y radio
; por consiguiente, una rama de la curva en el plano xy
es aproximadamente un óvalo circular asintótico al cilindro de eje el eje z
y radio ![]() en el interior del cual están contenidas las superficies. En
efecto, cuando
en el interior del cual están contenidas las superficies. En
efecto, cuando ![]() , la ecuación (70.7) tiende a
convertirse en la x2 + y2 = C. Cuanto mayor sea C,
mayores son los valores de x y de y que satisfacen la ecuación y
más pequeño es
, la ecuación (70.7) tiende a
convertirse en la x2 + y2 = C. Cuanto mayor sea C,
mayores son los valores de x y de y que satisfacen la ecuación y
más pequeño es ![]() , y el óvalo es más circular.
, y el óvalo es más circular.
Para valores pequeños de x y de y
que satisfacen (71.7) el primer y segundo términos son
poco importantes y la ecuación puede escribirse
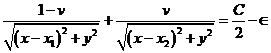 (72.7)
(72.7)
ecuación de la curva equipotencial para los dos
centros de fuerza 1 - v y v. Si C es grande, se compone de
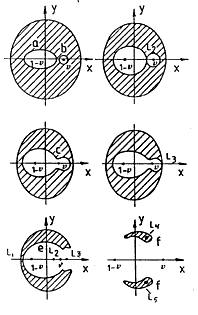
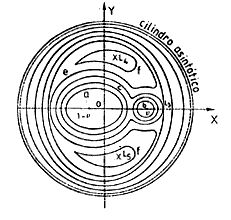
dos óvalos cerrados alrededor de cada uno de los centros 1 – v y v (a,b Fig. 5.7). Para
valores pequeños de C estos óvalos tienen tendencia a unirse entre sí.
Hay un valor determinado de C para el cual los óvalos que envuelven 1 - v
y v se encuentran en un punto doble L2 en el cual tienen una tangente común.
Si el valor de C se hace más pequeño, los óvalos se unen para formar una
superficie única con un cuello estrecho, indicada por C en la Fig. 5.7, por donde es posible que la partícula escape de la
proximidad de una de las masas finitas hacia la otra, pero todavía no es
posible que escape a la otra región. Para un nuevo decrecimiento de C,
la región interior encuentra a la exterior en un nuevo punto doble L3.
Si C sigue decreciendo, se halla otro punto doble L1,
mientras que el ensanchamiento del cuello en torno a L3 proporciona
a la partícula de masa infinitesimal la posibilidad de salir de la región que
envuelve las dos masas finitas (e en Fig. 5.7). Si el
proceso de decrecimiento de C continúa, las regiones inaccesibles para
la partícula m3 sobre el plano xy se encogen hasta
quedar reducidas a dos puntos, L4 y L5 (f
en Fig. 5.7).
FIG. 5.7
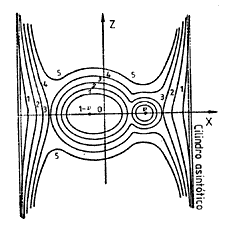
En la Fig. 6.7 se
representan simultáneamente todas las curvas que hemos ido considerando.
Para obtener las intersecciones de las superficies con el plano xz
haremos
y = 0 en la ecuación (70.7),
con lo que obtendremos
FIG. 6.7
FIG. 7.7
Para valores muy grandes de
x y de z que satisfagan esta ecuación, el segundo y tercer
términos no son muy importantes y podremos escribir
![]()
que es la ecuación de un
par de rectas paralelas al eje z. Cuanto mayor sea C mayor es el valor de x que
para un dado valor de z satisface la ecuación y menor es el valor de ![]() . Las rectas que corresponden al valor máximo de C son
generatrices del cilindro asintótico. Para valores pequeños de x y de z que
satisfagan la ecuación (73.7) podernos escribir
. Las rectas que corresponden al valor máximo de C son
generatrices del cilindro asintótico. Para valores pequeños de x y de z que
satisfagan la ecuación (73.7) podernos escribir
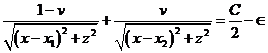 (74.7)
(74.7)
Volvemos a encontrar la ecuación de las curvas
equipotenciales que tienen las mismas propiedades que las anteriores. Por
consiguiente, la forma de las curvas en el plano xz es cualitativamente
la dada en la Fig. 7.7, donde los números 1, 2, ... indican
las curvas que corresponden a distintos valores decrecientes de C.
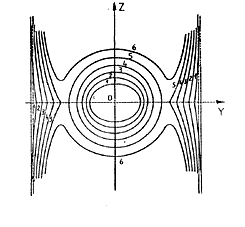
FIG. 8.7
FIG. 9.7
Haciendo x = 0 en la ecuación (70.7) obtenemos
la ecuación de las curvas de intersección de las superficies y el plano yz,
esto es:
Para valores muy grandes de y y de z
que satisfagan la ecuación (75.7) el segundo y tercer
términos son poco importantes y podemos escribir
![]()
que es la ecuación de un
par de líneas próximas a las generatrices del cilindro asintótico y que se
aproximan a él cuando C aumenta. Si 1 – v es mucho mayor que v,
el valor numérico de x2 es mucho mayor que el de x1;
por consiguiente, para pequeños valores de y y de z que
satisfagan (75.7) dicha ecuación se podrá escribir
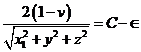
que es la ecuación de un círculo de radio
tanto mayor cuanto menor sea C. La forma de las curvas en el plano yz
es cualitativamente la representada en la Fig. 8.7, donde
los números 1,2,... indican, como antes, las curvas que corresponden a
distintos valores decrecientes de C.
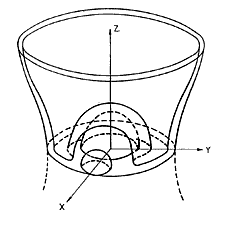
Es evidente, después del estudio
efectuado, que las superficies de Hill para distintos valores de C
consistirán, si C es grande, de dos superficies cerradas,
aproximadamente esféricas, que envuelven cada una de las masas finitas, metidas
dentro de un conjunto de superficies que cuelgan a modo de cortinas de un
cilindro asintótico simétrico con respecto al plano xy; conforme el
valor de C va disminuyendo, las superficies esféricas se van expandiendo
y acercando una a la otra hasta unirse para después, formando ya una sola
superficie y para valores de C todavía más pequeños, encontrarse con las
“cortinas”, estando los primeros puntos de contacto en el plano xy. Para
valores de C suficientemente pequeños, las superficies constan de dos
partes simétricas respecto al plano xy, sin puntos comunes. En la Fig. 9.7 damos un esquema simplificado de la forma de estas
superficies.
Hallada la forma de las superficies de Hill, podemos ver en que regiones
del espacio relativo se puede mover la partícula de masa infinitesimal. La
ecuación (64.7) nos da el cuadrado de la
velocidad y ya hemos dicho que para que la velocidad sea real debe ser 2U
> C. Si esto ocurre en el interior de una superficie cerrada ocurrirá en
cualquier otro punto interior a ella ya que la función cambia de signo
solamente en una superficie de velocidad relativa cero (2U = C).
Es evidente que podemos tomar un punto tan cerca de 1 - v o de v,
o lo que es lo mismo, ρ1 o ρ2 tan
pequeños que por grande que sea C, se verifique que 2U > C; en
este caso el movimiento será real en el interior de una de las dos superficies
esferoidales cerradas que envuelven las masas finitas o, si C no es tan
grande, en la superficie cerrada que envuelve las dos masas finitas. Por otro
lado, en la ecuación (64.7) podemos tomar x
e y suficientemente grandes para que, por grande que sea C, se
verifique que 2U > C, en cuyo caso la partícula de masa infinitesimal
estará muy alejada de las masas finitas y el movimiento será real en el espacio
exterior.
Veamos una aplicación de lo estudiado al
caso del movimiento de la Luna alrededor de la Tierra: Si se supone la órbita
de la Tierra circular y la masa de la Luna infinitesimal, se demuestra,
calculando el valor de C, que la Luna se mueve en el interior de una
superficie cerrada esferoidal que envuelve la Tierra. Por consiguiente, la Luna
no puede atravesar esta superficie de velocidad cero y en consecuencia no puede
alejarse indefinidamente de la Tierra. Basándose en esta propiedad Hill
demostró que la distancia de la Luna a la Tierra tiene un límite superior.
7.5.5
Puntos dobles de las superficies V = 0
Se deduce
de la expresión general de las superficies de velocidad relativa nula que los
puntos dobles que presentan cuando C disminuye están todos en el plano xy.
Por consiguiente, es suficiente para su estudio considerar la ecuación de las
curvas en el plano xy (ver 71.7). Como hemos
visto, hay tres puntos dobles en el eje x que aparecen cuando los óvalos
que circundan las masas finitas para un determinado valor de C se tocan
(L2) y para otros valores de C tocan la curva exterior
que los incluye (L1, L3); hay otros dos
puntos dobles que aparecen cuando, para un valor de C muy pequeño, las
superficies se encogen hasta desaparecer del plano xy en los dos puntos
(L4, L5) que forman triángulo equilátero
con los puntos ocupados por las masas finitas. Estos cinco puntos dobles
reciben el nombre de puntos de Lagrange y están relacionados con
importantes propiedades dinámicas del sistema.
Escribamos la
ecuación (71.7) en la forma
Las condiciones para que
presente puntos dobles son:
pero los primeros miembros de estas ecuaciones representan las derivadas
de
por consiguiente, recordando (62.7) y tomando
n = 1 podemos escribir
Las
expresiones ![]() y
y ![]() son proporcionales a
los cosenos directores de la normal a cualquier punto ordinario de las curvas y
puesto que
son proporcionales a
los cosenos directores de la normal a cualquier punto ordinario de las curvas y
puesto que ![]() e
e ![]() son nulos en las
superficies de velocidad nula se deduce que las direcciones de la aceleración
o líneas de fuerza efectiva son ortogonales a las superficies de velocidad
relativa nula. Por consiguiente, si un cuerpo de masa infinitesimal se coloca
en una superficie de velocidad relativa nula, empezará su movimiento en la
dirección de la normal; pero, en un punto doble el sentido de la normal resulta
ambiguo, de aquí que puede suponerse que si este cuerpo de masa infinitesimal
fue colocado en uno de estos puntos, en él permanecerá relativamente en reposo.
son nulos en las
superficies de velocidad nula se deduce que las direcciones de la aceleración
o líneas de fuerza efectiva son ortogonales a las superficies de velocidad
relativa nula. Por consiguiente, si un cuerpo de masa infinitesimal se coloca
en una superficie de velocidad relativa nula, empezará su movimiento en la
dirección de la normal; pero, en un punto doble el sentido de la normal resulta
ambiguo, de aquí que puede suponerse que si este cuerpo de masa infinitesimal
fue colocado en uno de estos puntos, en él permanecerá relativamente en reposo.
Las condiciones
impuestas por (76.7) y (77.7)
suponen también teniendo en cuenta (79.7) que ![]() e
e ![]() son nulas. Por tanto,
si el cuerpo de masa infinitesimal se coloca en un punto doble con velocidad
relativa nula, sus coordenadas verifican idénticamente las ecuaciones diferenciales
del movimiento y permanecerá siempre relativamente en reposo a menos que sea
perturbado por fuerzas exteriores al sistema considerado.
son nulas. Por tanto,
si el cuerpo de masa infinitesimal se coloca en un punto doble con velocidad
relativa nula, sus coordenadas verifican idénticamente las ecuaciones diferenciales
del movimiento y permanecerá siempre relativamente en reposo a menos que sea
perturbado por fuerzas exteriores al sistema considerado.
Sean las ecuaciones (77.7)
la segunda de las cuales se satisface para y = 0. Los puntos dobles
sobre el eje x vendrán determinados por las condiciones
Es fácil ver que el primer miembro de la primera
ecuación, considerado como una función de x, cambia de signo una sola
vez entre ![]() y x2,
entre x2 y
x1 y entre xl y
y x2,
entre x2 y
x1 y entre xl y ![]() . Por consiguiente hay tres puntos dobles sobre el eje x
en dichos intervalos. Designémosles por L1, L2
y L3, respectivamente.
. Por consiguiente hay tres puntos dobles sobre el eje x
en dichos intervalos. Designémosles por L1, L2
y L3, respectivamente.
Supongamos
que la distancia
entre v y el punto doble Ll
es ρ. Entonces, x - x2 = ρ, x
- x1 = ρ1 = 1 + ρ, x
= 1 - v + ρ. La ecuación que estamos considerando se puede
escribir, sustituyendo todos los términos en función de ρ y
quitando denominadores, de la forma
ecuación con una sola raíz real positiva
ya que sólo presenta una variación en el signo de sus coeficientes. El valor de
esta raíz depende de v. Si ![]() = 0, obtenemos
= 0, obtenemos
![]()
ecuación que tiene la raíz triple ρ = 0 y otras dos imaginarias
conjugadas. Si v ![]() 0, para un valor dado
de
0, para un valor dado
de ![]() suficientemente
pequeño, tres raíces de la ecuación (81.7) se pueden
expresar por medio del desarrollo en serie de potencias de v1/3
suficientemente
pequeño, tres raíces de la ecuación (81.7) se pueden
expresar por medio del desarrollo en serie de potencias de v1/3
correspondiendo al valor real de v1/3
un valor real de ρ y a los dos valores complejos de v1/3
dos valores complejos de ρ. Sustituyendo el valor de ρ
dado por (82.7) en (81.7) e
igualando a cero los coeficientes de las distintas potencias de v1/3,
se halla:
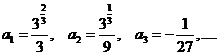
Por consiguiente
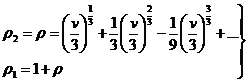 (83.7)
(83.7)
Representemos ahora
por ρ la
distancia de v al
punto doble L2. Ahora x
– x2 = - ρ, x
– x1 = ρ1 = 1 - ρ, x = (1- v) - ρ. Por
tanto, la primera ecuación de (80.7) resulta:
![]() (84.7)
(84.7)
Resolviéndola como en el caso anterior se halla:
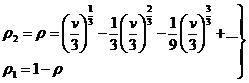 (85.7)
(85.7)
Finalmente llamemos 1 - ρ a la
distancia entre 1 - v y el punto doble L3. En este
caso tendremos x - x2 = -2 + ρ, x –
x1 = -1 + ρ, x = -v - 1 + ρ y la primera ecuación de (80.7)
se escribirá
Si v = 0 esta
ecuación resulta
![]()
que tiene una raíz simple ρ =
0. Si v ![]() 0, ρ
se puede expresar por medio de un desarrollo en serie de potencias de v que
converge para valores de v suficientemente pequeños:
0, ρ
se puede expresar por medio de un desarrollo en serie de potencias de v que
converge para valores de v suficientemente pequeños:
![]() (87.7)
(87.7)
Sustituyendo este valor de ρ en (86.7), operando e igualando a cero los coeficientes de las
distintas potencias de v, hallamos
![]()
con lo cual
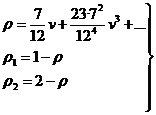 (88.7)
(88.7)
Para hallar los puntos dobles L4 y
L5 situados fuera del eje x consideremos otra vez las
ecuaciones (77.7). Puesto que ahora es y ![]() 0, podemos dividir por
y la segunda ecuación, obteniendo
0, podemos dividir por
y la segunda ecuación, obteniendo
Multiplicando (89.7)
primero por x - x2 y después por x - x1
y restando cada uno de los productos resultantes, separadamente, de la
primera de (77.7), se obtiene
Pero, x2 = 1- v, x1
= -v y
x2 - x1 = 1; por tanto, las
ecuaciones (90.7) se reducen a
siendo las soluciones reales de (91.7)
ρ1 = ρ2 = 1. Por consiguiente,
los puntos L4 y L5 forman sendos triángulos
equiláteros con los cuerpos de masa finita.
7.5.6 La estabilidad
de los puntos de Lagrange
Hemos hallado cinco soluciones particulares del
movimiento del cuerpo de masa infinitesimal. Si dicho cuerpo se desplaza un
poco de uno de los puntos de Lagrange debido a alguna perturbación producida
por alguna causa distinta de la atracción de las dos masas finitas, puede
ocurrir que adquiera una velocidad tal que salga despedido alejándose
rápidamente del punto de Lagrange o que la velocidad que adquiera sea tal que haga
que se quede oscilando en torno a dicho punto. En el primer caso decimos que la
solución es inestable y en el segundo caso que estamos ante una
solución estable.
Supongamos que la posición de un punto de Lagrange
en el sistema de coordenadas que gira es (x0, y0)
y representemos por (x0 +![]() , y0 +
, y0 +![]() ,
, ![]() ) la
posición del cuerpo de masa infinitesimal cuando se ha desplazado respecto al
punto de Lagrange con una velocidad
) la
posición del cuerpo de masa infinitesimal cuando se ha desplazado respecto al
punto de Lagrange con una velocidad ![]() . Sustituyendo los valores de la posición y la velocidad en
las ecuaciones del movimiento (62.7) para n
= 1 y desarrollando en serie obtendremos:
. Sustituyendo los valores de la posición y la velocidad en
las ecuaciones del movimiento (62.7) para n
= 1 y desarrollando en serie obtendremos:
donde el subíndice 0 indica el valor de las
derivadas en el punto (x0, y0, z0).
Si los desplazamientos ![]() ,
, ![]() ,
, ![]() son pequeños podemos despreciar los términos
del desarrollo a partir del segundo grado en
son pequeños podemos despreciar los términos
del desarrollo a partir del segundo grado en ![]() ,
, ![]() ,
, ![]() y escribir las relaciones (92.7)
en la forma
y escribir las relaciones (92.7)
en la forma
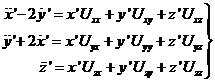 (93.7)
(93.7)
donde, tanto las derivadas ![]() como U se
calculan para el punto de Lagrange (x0, y0,
z0).
como U se
calculan para el punto de Lagrange (x0, y0,
z0).
Consideremos, de momento, que nos situamos
en el plano xy. Tendremos:
sistema de ecuaciones diferenciales lineales a coeficientes constantes
cuya solución general es
donde las αi son constantes de integración, las βi
son constantes que dependen de ellas y de los coeficientes que aparecen en
(94.7) y las λi son raíces
del determinante característico
cuyos elementos son los coeficientes de α
y β en las ecuaciones que se obtienen al sustituir en (94.7) las soluciones de la forma
![]()
Si
todas las soluciones λi obtenidas de la ecuación
(96.7) son imaginarias puras, ![]() e
e ![]() se expresan mediante funciones periódicas
estables en las proximidades de (x0, y0, z0).
Si algunas de las soluciones λi son reales o complejas,
se expresan mediante funciones periódicas
estables en las proximidades de (x0, y0, z0).
Si algunas de las soluciones λi son reales o complejas,
![]() e
e ![]() crecen con el tiempo y la solución es
inestable.
crecen con el tiempo y la solución es
inestable.
Puede suceder que algún término de (95.7) sea constante (λi = 0).
En este caso, si el resto de las λi son imaginarias
puras, la solución es también estable.
Recordemos que ![]() con
con
![]()
y hagamos
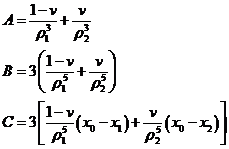
hallaremos:
En las soluciones L1,
L2, L3 es y0 = z0 = 0
de modo que
![]()
Por consiguiente, por una parte
![]()
y por otra, las ecuaciones del movimiento para un pequeño desplazamiento se
reducen a
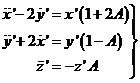 (98.7)
(98.7)
La tercera ecuación es independiente de las otras dos.
Su solución es
![]()
que nos dice que la oscilación en la dirección de z
es finita y pequeña con periodo ![]() .
.
Sustituyendo los valores de Uxx, Uyy y Uzz
en el determinante (96.7) y operando, obtenemos
A cada punto alineado de Lagrange corresponderá un
valor de A; por tanto, tendremos tres ecuaciones en λ, una
para cada uno de los puntos L1, L2, L3,
de la forma (99.7). Se puede probar que para valores
pequeños de v y, para cualquiera de las tres A se verifica:
![]()
En
consecuencia, la ecuación bicuadrada (99.7) considerada
como en λ2 tiene dos raíces reales opuestas y la
ecuación en λ4 tendrá cuatro raíces, dos reales y dos
imaginarias conjugadas siendo las raíces de cada par iguales en valor absoluto
pero de signos opuestos. Luego, las soluciones correspondientes a los puntos
alineados son inestables. Sin embargo, escogiendo convenientemente los valores
iniciales de x’, y’ y z’ el movimiento puede llegar a ser
periódico, moviéndose el cuerpo de masa infinitesimal alrededor del punto de
Lagrange en una trayectoria elíptica. De todos modos, en general, el caso
colineal debe considerarse inestable.
Sea
ahora las soluciones en triángulo equilátero que dan los puntos de Lagrange L4
y L5. En este caso ![]() z0=0.
Tomando el punto L4 tenemos, sustituyendo en (97.7) y recordando que xl = - v,
x2 =
1 - v:
z0=0.
Tomando el punto L4 tenemos, sustituyendo en (97.7) y recordando que xl = - v,
x2 =
1 - v:
Las ecuaciones del movimiento para un pequeño desplazamiento resultan ser:
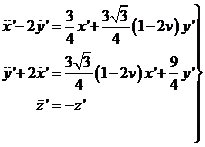 (101.7)
(101.7)
Observamos que también en este caso la oscilación en la dirección de z’
es estable, viniendo dada por
![]()
donde C3 y C4 son
constantes de integración, siendo el periodo 2π.
Sustituyendo los valores (100.7) en la ecuación (96.7) y operando se obtiene
![]()
La condición para que las cuatro raíces de esta ecuación bicuadrada sean
imaginarias puras, conjugadas dos a dos, es que
![]()
Si
hacemos
![]()
obtenemos la ecuación
![]()
cuyas soluciones son
![]()
Recordando que ![]() , tomaremos la raíz que corresponde al signo menos.
, tomaremos la raíz que corresponde al signo menos.
Cuando sea ![]() = 0, será v =
0.0385. Por tanto, para que el punto de Lagrange sea estable debe ser
= 0, será v =
0.0385. Por tanto, para que el punto de Lagrange sea estable debe ser
El razonamiento que hemos hecho se puede
aplicar sin más que tomar ![]() ,
, ![]() , z = 0, al punto L5. Por
tanto, si se satisface la condición (102.7) existen
alrededor de L4 y L5 cuerpos
de masa infinitesimal que describen órbitas periódicas.
, z = 0, al punto L5. Por
tanto, si se satisface la condición (102.7) existen
alrededor de L4 y L5 cuerpos
de masa infinitesimal que describen órbitas periódicas.
Aplicación al Sistema Solar: Después de haberse hallado las
soluciones en línea recta y en triángulo equilátero del problema de los tres cuerpos
que acabamos de exponer, se creyó durante algún tiempo que eran meras
soluciones matemáticas, muy interesantes pero que no tendrían nunca aplicación
astronómica ya que parecía muy improbable que pudieran existir tales
formaciones en la naturaleza. Sin embargo, tales soluciones se dan en el
Sistema Solar. En efecto, si tomamos como masas principales m1
y m2 el Sol y Júpiter, respectivamente, se
verifica que ![]() de modo que se
satisface la condición de estabilidad (102.7),
hallándose alrededor de los puntos L4 y L5
dos grupos de asteroides (Troyanos y Griegos) en oscilación,
proporcionando cada uno de ellos con el Sol y Júpiter un ejemplo de solución en
triángulo equilátero.
de modo que se
satisface la condición de estabilidad (102.7),
hallándose alrededor de los puntos L4 y L5
dos grupos de asteroides (Troyanos y Griegos) en oscilación,
proporcionando cada uno de ellos con el Sol y Júpiter un ejemplo de solución en
triángulo equilátero.
Por
otra parte, Kordelewski sugirió que en el sistema Tierra-Luna los puntos L4
y L5 están ocupados por partículas meteóricas
que aparecen, en muy buenas condiciones de visibilidad, como unas ténues
nebulosidades. Otro ejemplo lo tenemos en el descubrimiento por parte del
Voyager 1 en su viaje hacia Saturno: El satélite Dione B Helena orbita a la
misma distancia de Saturno que de Dione oscilando alrededor de un punto
avanzado 60º con respecto a Dione.
Con respecto a las soluciones en línea recta, si m1 y m2
son el Sol y la Tierra, respectivamente, en el punto de Lagrange L3,
opuesto al Sol, aparece una débil luminosidad visible después de la puesta del
Sol en el plano de la eclíptica. El fenómeno recibe el nombre de “Gegenschein”
y se cree que es debido a la iluminación por el Sol de una acumulación de
partículas meteóricas en el citado punto de Lagrange.