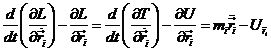7.1 Ecuaciones del movimiento
Consideremos n puntos
materiales (n > 2) Pi ( i=1,2,...,n)
de masas respectivas mi (i=1,2,...n) referidos
a un sistema de coordenadas cartesianas fijo al que asociamos la variable
tiempo t de manera que las posiciones de los puntos Pi
estén definidas por los vectores ![]() de componentes rij
(i= 1,2,...,n; j=1,2,3). Supongamos que la acción mútua entre dos puntos Pi, Pk tiene por dirección la recta que los une
y por módulo G mi mk |f(rik)|, donde G es la constante de la
gravitación universal, rik la distancia entre Pi y
Pk y f(rik) una cierta función de dicha distancia, estando
el sentido de la fuerza que Pk
ejerce sobre Pi. definido por el
vector
de componentes rij
(i= 1,2,...,n; j=1,2,3). Supongamos que la acción mútua entre dos puntos Pi, Pk tiene por dirección la recta que los une
y por módulo G mi mk |f(rik)|, donde G es la constante de la
gravitación universal, rik la distancia entre Pi y
Pk y f(rik) una cierta función de dicha distancia, estando
el sentido de la fuerza que Pk
ejerce sobre Pi. definido por el
vector![]() con
rik=| rik
|. Incluiremos en la función f(rik) el signo correspondiente que será
negativo para las fuerzas repulsivas y positivo para las atractivas.
con
rik=| rik
|. Incluiremos en la función f(rik) el signo correspondiente que será
negativo para las fuerzas repulsivas y positivo para las atractivas.
Las ecuaciones del movimiento
del punto Pi serán:
habiendo hecho G=1 con el consiguiente cambio de la variable tiempo
que seguiremos llamando t.
Introduzcamos las funciones escalares energía
cinética T y función de fuerzas U dadas por las expresiones
donde
Si derivamos parcialmente la función U con
respecto a una cualquiera de las componentes rij
tendremos:
![]() (5.7)
(5.7)
que nos da para el gradiente ![]() , teniendo en cuenta (1.7), la expresión
, teniendo en cuenta (1.7), la expresión
La función lagrangiana
L = T + U
verifica, evidentemente las ecuaciones
A partir de (7.7) podemos
obtener la formulación canónica del problema. En efecto, sea ![]() el momento
correspondiente a
el momento
correspondiente a ![]() ,
,
y H la función hamiltoniana
H = T - U
Teniendo en cuenta (8.7) y
que (2.7) se puede escribir ahora
![]()
se obtienen las igualdades
![]()
![]()
![]()
que constituyen
las ecuaciones canónicas del movimiento
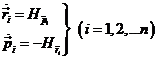 (9.7)
(9.7)
llamadas ecuaciones de Hamilton-Jacobi,
equivalentes a las (1.7) y (6.7).