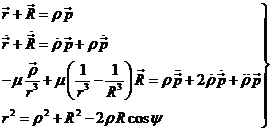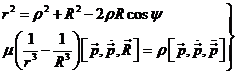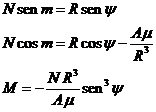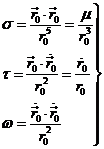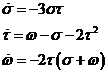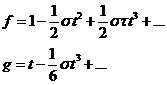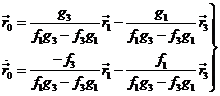6.2 Método de Laplace

El método de Laplace consiste en determinar por medio de las tres A_i y las tres D_i ( i = 1, 2, 3 ) observadas, las coordenadas heliocéntricas y las componentes de la velocidad del cuerpo en una época dada (por ejemplo, el momento de la segunda observación) y obtener después sus elementos orbitales a partir de y , teniendo en cuenta que se mueve bajo la acción de una fuerza conocida (atracción solar).

Supongamos realizada una observación y derivemos dos veces la relación (1.6) con respecto al tiempo:

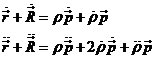
La Tierra y el cuerpo celeste en cuestión se mueven sujetos a la atracción gravitatoria del Sol y sus masas pueden despreciarse comparadas con la masa del Sol. Por consiguiente (Ap. 3.2):

(4.6)

donde m = GM ( G = constante de la gravitación universal y M = masa del Sol ).

Sumando miembro a miembro las (4.6) obtenemos:

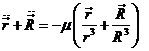
o lo que es lo mismo:

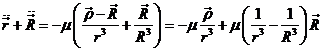(5.6)

Por otra parte, de la Fig. 1.6 obtenemos:

(6.6)

donde y es el ángulo entre los vectores y .

Pues bien, las fórmulas básicas del método de Laplace son:

(7.6)

Las ecuaciones (7.6) representan el aspecto geométrico y gravitacional del movimiento. Contienen el valor deducido de la observación en un instante t = t₀ y sus derivadas primera y segunda en este mismo instante que deberemos calcular a partir de .

Designemos con el subíndice “cero” el valor de y sus derivadas en el instante t = t₀ . Desarrollando en serie de Taylor el valor de , tendremos:

(8.6)

y despreciando los términos con potencias en t ³ 3, conocida la observación en el instante t_i ( i = 1, 2, 3 ) pueden obtenerse , , mediante el sistema:

(9.6)

Los valores que se obtienen son sólo aproximados puesto que hemos truncado la serie en los términos de segundo grado en t al necesitar sólo derivadas de hasta el segundo orden. Se podrían obtener valores más aproximados de y tomando más términos en la serie (8.6) aunque no se necesiten derivadas de orden superior al segundo en las ecuaciones (7.6). También si se dispone de más observaciones, se pueden añadir ecuaciones y proceder a resolver el sistema por mínimos cuadrados. Pero, como que más tarde habremos de corregir de aberración, tomaremos, por comodidad, el sistema (9.6) de tres ecuaciones con tres incógnitas y lo resolveremos algebraicamente. Por otra parte, es posible escoger t₀ de modo que el error sea mínimo, pero se suele tomar t₀ de forma que sea el tiempo de la segunda observación.

Supongamos ahora que hemos encontrado y . Multipliquemos escalarmente la tercera de (7.6) primero por y después por. Obtendremos:

(10.6)

y

(11.6)

Tomando la última ecuación de (7.6) y (10.6) formaremos el sistema:

(12.6)

que resuelto algebraicamente nos dará las incógnitas r y p.

Es facil ver que la ecuacion que resulta al eliminar una de las incógnitas en dicho sistema es algebraica de octavo grado en la otra. Para simplificar su resolución se suele introducir el ángulo auxiliar f formado por los vectores y (Fig. 1.6) que la reduce a una de cuarto grado. En efecto, en el triángulo PST de dicha figura 1.6 tenemos:

(13.6)

Escrita la segunda de (12.6) en la forma

(14.6)

con

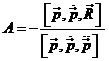(15.6)

y teniendo en cuenta (13.6), resulta:

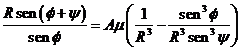
y desarrollando y agrupando términos:

(16.6)

Haciendo para simplificar

(17.6)

donde el signo de N se toma de modo que M sea positivo, y sustituyendo en (16.6) se obtiene:

(18.6)

que puede proporcionar a lo sumo dos soluciones f, en cuyo caso la discriminación suele hacerse tomando alguna nueva observación.

El cálculo de f se efectúa por aproximaciones sucesivas a partir de un primer valor obtenido gráficamente o por medio de tablas.

La discusión de la ecuación (18.6) puede hallarse en cualquiera de los textos de Mecánica Celeste que damos en la Bibliografía.

Si sustituimos el valor de f obtenido de (18.6) en (13.6) obtendremos r y r.

Con r la ecuación (11.6) nos dará .

Hallados r y las dos primeras de (7.6) nos darán y a partir de los cuales calcularemos los elementos de la órbita.

6.2.1 Corrección de aberración

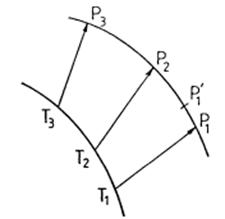
FIG. 2.6

Recordemos que debido a la finitud de la velocidad de propagación de la luz los astros no se ven desde la Tierra en la posición que ocupan en el instante de la observación (Ap. 4.2). Por tanto, obtenido un primer valor de r tendremos que corregir de aberración planetaria. Esta corrección afectará las coordenadas observadas y tendremos que volver a plantear el problema a partir de (7.6). En la práctica lo que se hace es corregir los tiempos de las observaciones. Sean T_i ( i = 1, 2, 3) las posiciones del centro de la Tierra en los instantes t_i de las observaciones. El cuerpo P pasa por los puntos P₁, P₂, P₃ (Fig.2.6) no en los tiempos t₁, t₂, t₃ sino en dichos tiempos disminuidos en el tiempo t_i en que la luz tarda en ir de P_i a T_i ( i = 1, 2, 3). Para hacer estas correcciones a los tiempos de observación es necesario conocer las distancias T_iP_i = r_i ( i = 1, 2, 3). Teniendo en cuenta que conocemos un primer valor de r y , podremos escribir con suficiente aproximación

Supongamos que C representa la velocidad de la luz. Las épocas en que el cuerpo P estaba en P₁, P₂, P₃ son:

( i = 1 ,2,3 )

Estas correcciones deben introducirse en el sistema (9.6) con lo cual obtendremos unos nuevos valores de y que nos conducirán a nuevos valores de r y . Si éstos no difieren mucho de los encontrados anteriormente se podrá seguir el cálculo. Si no, deberemos realizar todavía una nueva corrección de aberración.

6.2.2 Corrección de los elementos. Método de Leuschner

Aunque efectuemos la corrección de aberración a la que nos acabamos de referir, una vez calculados los elementos orbitales a partir de los y correspondientes a la época de la segunda observación y calculada una efemérides para las épocas primera y tercera, encontraremos discrepancias entre observación y cálculo para dichas épocas. Esto es debido a las aproximaciones que conlleva el método que estamos empleando. Deberemos pues, corregir los elementos de la órbita. Leuschner (1902) introdujo, basándose en trabajos realizados anteriormente por Harzer (1896), un procedimiento para hallar , y , correspondientes a las épocas primera y tercera a partir de las y de la segunda observación, y una vez hallados poder corregir , antes de obtener los elementos orbitales, lo cual simplifica muchísimo el proceso de cálculo.

Seguiremos indicando con el índice “cero” todos los valores correspondientes a la segunda observación. Si es el vector de posición en la época t, podemos expresarlo mediante desarrollo en serie de potencias de t en la forma:

(19.6)

Definamos las cantidades s, t, w por

(20.6)

Derivándolas y utilizando la ecuación del movimiento

(21.6)

para eliminar tendremos:

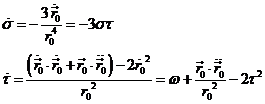
y multiplicando escalarmente por (21.6) y dividiendo luego por :

con lo que será:

Finalmente:

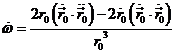
multiplicando ahora por (21.6) obtenemos:

y por otra parte el segundo término de es

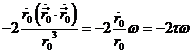
con lo que:

En resumen, pues, nos quedan las relaciones:

(22.6)

Entonces, a partir de la ecuación (21.6) obtendremos, derivando sucesivamente y teniendo en cuenta (22.6):

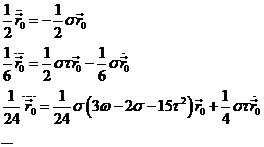
Sustituyendo estas expresiones en (19.6) obtendremos, finalmente:

(23.6)

donde:

(24.6)

Estas series, llamadas simplemente series f y g, convergen rápidamente para valores pequeños de t y nos permiten hallar conocidos los valores y correspondientes a la segunda observación.

Para mejorar los valores y podemos proceder de la siguiente forma: Con y calcularemos s, t, w mediante las fórmulas (20.6). Sustituidos estos valores en (24.6) haciendo t = t₁ y t = t₃ obtendremos los pares de valores f₁, g₁ y f₃, g₃, que sustituidos en (23.6) nos proporcionarán y .

Con y obtendremos r₁ y r₃ de las fórmulas

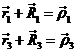
y hallados los módulos de y , podremos calcular:

Estos y son calculados. Nosotros teníamos los vectores proporcionados por la observación, de modo que si llamamos a los primeros y a los segundos, tendremos:

De aquí que, si llamamos, en general, a este será

de donde

que podremos escribir para 1 y 3.

De esta forma tendremos unos nuevos valores de correspondientes a la primera y tercera observaciones:

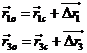
Por otra parte, si de

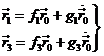(25.6)

despejamos y , tendremos:

(26.6)

y si en y en (26.6) escribimos y , respectivamente, obtendremos valores más aproximados de y con los cuales volveremos a recalcular s, t, w, f₁, f₃, g₁, g₃, r₁, r₃, y , y con el sistema (26.6) obtendremos nuevos valores, más aproximados, y .

Cuando observemos que los últimos valores hallados no difieren sensiblemente de los anteriores podemos ya proceder a calcular con ellos los elementos orbitales.

Para la obtención de los elementos orbitales a partir de y remitimos al lector al Apartado 3.11.4.

ANTERIOR

ÍNDICE

SIGUIENTE