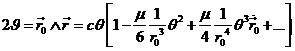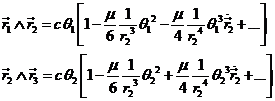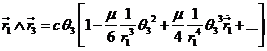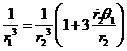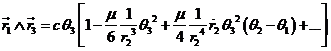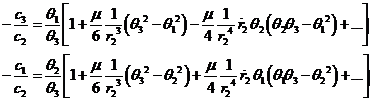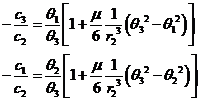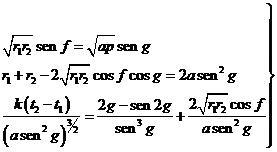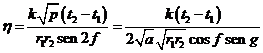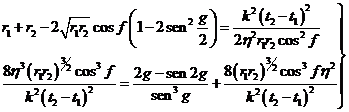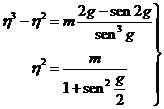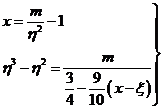6.3 Método
de Gauss
En el método de Gauss, al igual que hicimos en el de Laplace,
distinguiremos dos partes. En la primera, veremos cómo pueden calcularse tres
posiciones heliocéntricas del cuerpo cuya órbita tratamos de calcular a partir de
tres posiciones geocéntricas. En la segunda, estudiaremos la forma de obtener
los elementos orbitales a partir de dos de las tres posiciones heliocéntricas.
6.3.1
Determinación de las áreas triangulares
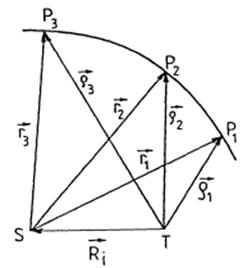
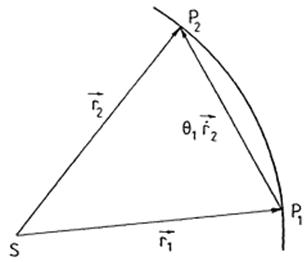
FIG. 3.6
Sean
(Fig. 3.6) T el
centro de la Tierra, Pi la
posición del cuerpo P en cuestión en
la época ti ( i = 1, 2, 3 ), S el Sol, ![]() el vector unitario en la dirección TPi que obtenemos por observación (recordemos Cap. 6.1),
el vector unitario en la dirección TPi que obtenemos por observación (recordemos Cap. 6.1), ![]() la posición
geocéntrica del Sol y
la posición
geocéntrica del Sol y ![]() la posición
heliocéntrica de Pi.
la posición
heliocéntrica de Pi.
Puesto que suponemos que la órbita es kepleriana, los vectores ![]() ( i = 1, 2, 3 ) son coplanarios, cumpliéndose:
( i = 1, 2, 3 ) son coplanarios, cumpliéndose:
donde c1, c2, c3 son tres escalares no simultáneamente
nulos.
Multiplicando
vectorialmente (27.6) primero por ![]() por la
izquierda y después por
por la
izquierda y después por ![]() por la derecha,
tendremos:
por la derecha,
tendremos:
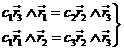 (28.6)
(28.6)
sistema que podemos escribir en la forma:
Si tomamos como sistema de referencia el de coordenadas P, Q, R, que hemos considerado ya otras
veces (Ap. 3.11.3), con origen el Sol,
resulta que los productos vectoriales que aparecen en los denominadores de (29.6) tienen, todos ellos, la dirección y sentido de un
vector unitario ![]() tomado sobre el eje R en el sentido positivo del mismo. Por
otra parte, podemos expresar mediante los llamados corchetes de Gauss
tomado sobre el eje R en el sentido positivo del mismo. Por
otra parte, podemos expresar mediante los llamados corchetes de Gauss ![]() el área del triángulo
determinado por los vectores
el área del triángulo
determinado por los vectores ![]() ( i, j = 1, 2, 3).
( i, j = 1, 2, 3).
En consecuencia, podremos escribir:
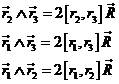 (30.6)
(30.6)
y, por tanto, (29.6) se
podrá expresar en la forma:
![]() (31.6)
(31.6)
De la Fig. 3.6 deducimos
![]() (32.6)
(32.6)
y multiplicando por ci y sumando teniendo en cuenta (27.6), obtenemos:
ecuación vectorial que equivale a un sistema de
tres ecuaciones escalares en las componentes de ![]() ,
, ![]() con las incógnitas ri, ci ( i
= 1, 2, 3).
con las incógnitas ri, ci ( i
= 1, 2, 3).
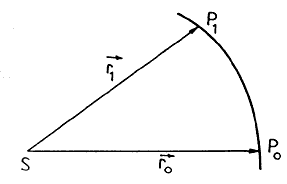
FIG.4.6
Para
determinar las ci (razones
entre las áreas) supondremos la órbita referida a los dos ejes rectangulares
heliocéntricos P,Q situados en su plano. Sean P0 y P1
las posiciones del cuerpo P en
los tiempos t0 y t0 + q; ![]() el área del triángulo P0SP1 y S el área del sector curvilíneo limitado por los
radios vectores
el área del triángulo P0SP1 y S el área del sector curvilíneo limitado por los
radios vectores ![]() y
y ![]() y el arco
de órbita
y el arco
de órbita ![]() (Fig.
4.6)
(Fig.
4.6)
Tendremos:
![]()
siendo c la constante de las áreas.
Escribiremos el desarrollo de ![]() en función del
tiempo q, basándonos en el desarrollo de
en función del
tiempo q, basándonos en el desarrollo de ![]() en función del tiempo
q en el entorno de
en función del tiempo
q en el entorno de ![]() :
:
![]() (34.6)
(34.6)
Multiplicando vectorialmente por la izquierda por ![]() :
:
cuyos
coeficientes calcularemos de la siguiente forma:
Para el primero, recordaremos que, según la ley de las áreas es
Para el segundo, multiplicaremos por ![]() por la izquierda la
ecuación del movimiento:
por la izquierda la
ecuación del movimiento:
El tercero, lo calcularemos derivando esta
última expresión:
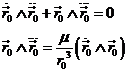
es decir:
Y, volviendo
a derivar, obtendremos el cuarto:
![]()
de donde:
Derivando la ecuación del movimiento y multiplicando
por ![]() :
:
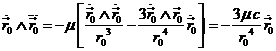
y sustituyendo en el segundo término del
segundo miembro de (39.6), obtenemos, finalmente:
Sustituyendo (36.6), (37.6), (38.6) y (40.6) en (35.6),
tendremos:
Apliquemos este resultado a las áreas triangulares determinadas por las
tres posiciones sucesivas de P, P1,
P2, P3, para las épocas tl, t2, t3. Sean ![]() ,
, ![]() y
y ![]() los
respectivos vectores de posición. Hagamos, por otra parte
los
respectivos vectores de posición. Hagamos, por otra parte
![]()
y tomemos como origen de tiempos t2 con
lo cual será ![]() y
y ![]() . Tendremos:
. Tendremos:
y si ahora tomamos como origen t1 con lo
que será ![]() , podremos escribir:
, podremos escribir:
6.3.2 Fórmulas
aproximadas de Encke
Hagamos las hipótesis simplificativas
siguientes:
FIG 5.6
1) Supongamos
que la velocidad entre Pl y P2 (Fig. 5.6)
es ![]() .
.
2) En
la expresión dada por el teorema del coseno
despreciemos ![]() .
.
3) Teniendo
en cuenta que ![]() de (44.6)
obtendremos:
de (44.6)
obtendremos:
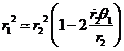
y elevando ambos miembros a -3/2, desarrollando el
segundo miembro por la fórmula del binomio de Newton y tomando sólo dos
términos del desarrollo:
4) Sustituyamos
(45.6) en (43.6) haciendo, además, r1 = r2 en los
términos de cuarto orden en el tiempo. Tendremos:
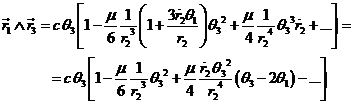
y teniendo en cuenta que
![]()
podremos escribir, finalmente:
Dividiendo las (42.6) por (46.6),
habida cuenta de las razones (29.6), obtendremos:
expresiones que nos dan, a menos de un factor
constante, los valores de las incógnitas ci
en función de r2.
Las fórmulas (47.6)
son poco prácticas al contener la derivada ![]() . Por este motivo, se suelen despreciar los términos a partir
del que contiene el factor
. Por este motivo, se suelen despreciar los términos a partir
del que contiene el factor ![]() , inclusive, con lo que queda:
, inclusive, con lo que queda:
que son las llamadas fórmulas aproximadas de Encke
6.3.3 Cálculo
de las ri y de las posiciones
heliocéntricas
Multiplicando (33.6)
escalarmente por ![]() obtendremos:
obtendremos:
![]()
dividiendo ambos miembros por -c2 y sustituyendo los cocientes ![]() y
y ![]() por los valores (47.6), resulta:
por los valores (47.6), resulta:
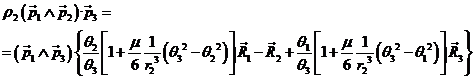 (49.6)
(49.6)
ecuación de la forma
con
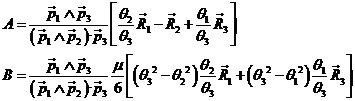
Resolviendo el sistema formado por la ecuación (50.6) y
se obtienen r2 y ![]() .
.
Al despejar una de las incógnitas de una
de las ecuaciones (50.6) o (51.6) y
sustituirla en la otra, se obtiene una ecuación de octavo grado análoga a la
que hemos encontrado al estudiar el método de Laplace (Ap.
6.2, fórmula 18.6).
Hallados r2 y r2 ,
sustituyendo el valor de r2 en (48.6)
obtendremos -c3/c2
y -c1/c2.
Dividiendo (33.6) por -c2, obtendremos:
ecuación vectorial que equivale a tres ecuaciones
escalares de las cuales obtendremos r1 y r3.
Finalmente, sustituyendo sucesivamente r1,
r2 y r3 en
![]()
obtendremos las tres posiciones heliocéntricas ![]() ,
, ![]() y
y ![]() .
.
6.3.4.
Corrección de aberración y de los
parámetros c1/ c2 ,
c3 /c2 .
La órbita que calculemos a partir de las posiciones heliocéntricas que
hemos encontrado deberá ser corregida. En primer lugar, tengamos en cuenta que
una vez hallado un primer valor de r deberemos corregir de aberración (ver 6.2.1). Corregido el tiempo de aberración y
obtenidos nuevamente c1/c2
y c3/c2
, una primera corrección de dichos parámetros puede obtenerse calculando
las razones
![]()
donde ![]() es el área del sector
limitado por los radios vectores
es el área del sector
limitado por los radios vectores ![]() ,
, ![]() y el arco de órbita
entre las posiciones Pi y Pj , y
y el arco de órbita
entre las posiciones Pi y Pj , y ![]() el área del triángulo SPiPj. En efecto,
el área del triángulo SPiPj. En efecto,
![]()
o sea:
![]()
y, análogamente:
![]() Estos cocientes nos proporcionarán, a partir de (52.6) valores más aproximados de r1 y r3 y en consecuencia de
Estos cocientes nos proporcionarán, a partir de (52.6) valores más aproximados de r1 y r3 y en consecuencia de ![]() y
y ![]() .
.
6.3.5 Cálculo de los elementos de una órbita por
dos posiciones heliocéntricas
|
FIG. 6.6 |
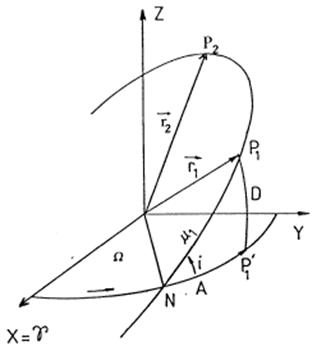
Supongamos conocidas dos posiciones heliocéntricas
P1 y P2 en las épocas tl y t2 por sus coordenadas ecuatoriales
heliocéntricas: ( ![]() , A1, Dl;
tl ), (
, A1, Dl;
tl ), (![]() , A2, D2;
t2 ).
, A2, D2;
t2 ).
Si t2 es posterior a t1 el movimiento será directo
respecto al plano ecuatorial si A2 >Al y retrógrado si A2
< A1. En el primer caso será i < 90º y en el segundo 90º
< i < 180º.
Del triángulo P1P1’ N de la Fig.6.6
y su análogo para la posición P2, deducimos:
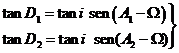
sistema de dos ecuaciones en las incógnitas i, W que nos darán estos dos elementos orbitales sin
ambigüedad puesto que conocemos el cuadrante en que se halla i.
También es inmediato el cálculo de los argumentos ![]() y
y ![]() por cualquiera de las
fórmulas
por cualquiera de las
fórmulas
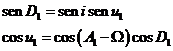
o sus análogas
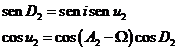
y puesto que se verifica
![]()
podremos calcular la diferencia entre las anomalías
verdaderas de las posiciones P2
y P1.
En resumen, el problema que tratamos de resolver
quedará reducido, a partir de ahora, a calcular los elementos a, e, w, T de una órbita de la que se conocen los radios
vectores ![]() y
y ![]() correspondientes a dos
épocas t1 y t2 y la diferencia
V2 - V1 de sus
anomalías verdaderas.
correspondientes a dos
épocas t1 y t2 y la diferencia
V2 - V1 de sus
anomalías verdaderas.
Supongamos
que la órbita es elíptica: Sean E1 y E2 las anomalías
excéntricas correspondientes a ![]() y
y ![]() . Hagamos:
. Hagamos:
![]()
y recordemos las siguientes fórmulas del movimiento
elíptico:
![]()
![]()
De la segunda, resulta:
![]()
y despejando ![]() :
:
![]()
Restando de 1 y sumando 1 a los dos miembros de
esta última igualdad, resulta:
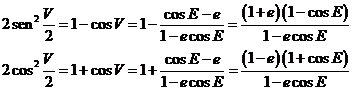
Cambiando 1-
ecosE por r/a y extrayendo la raiz cuadrada nos queda para
cada una de las posiciones P1 y P2:
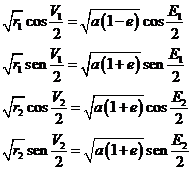
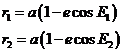
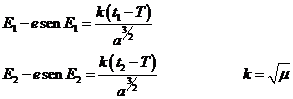
fórmulas de las
que se deducen, por simples transformaciones, las igualdades
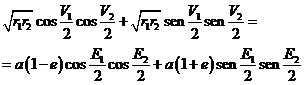
es decir:
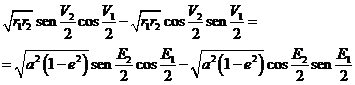
o sea:
![]()
o sea:
![]()
es decir, dividiendo los dos miembros por ![]() :
:
Las ecuaciones (53.6), (54.6),
(55.6) y (56.6) que resumimos a
continuación
constituyen un sistema de cuatro ecuaciones con
las incógnitas a,e,g y G. Eliminando ![]() entre la primera y la
tercera y
entre la primera y la
tercera y ![]() entre la primera y la
cuarta, nos queda el sistema:
entre la primera y la
cuarta, nos queda el sistema:
e introduciendo una nueva variable h definida por cualquiera de las
expresiones equivalentes
(obtenida la segunda sustituyendo ![]() por el valor de
por el valor de ![]() deducido de la primera
de (58.6)), y eliminando
deducido de la primera
de (58.6)), y eliminando ![]() entre (59.6) y las dos últimas de (58.6),
obtendremos:
entre (59.6) y las dos últimas de (58.6),
obtendremos:
Finalmente, si llamamos m
y l
a las constantes
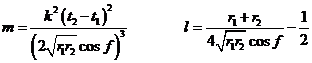
sustituyéndolas en las ecuaciones (60.6), dividiendo previamente la primera por ![]() , nos
queda
, nos
queda
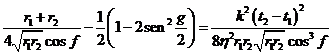
Las ecuaciones (61.6)
y (62.6) constituyen el sistema de ecuaciones de Gauss,
algebraicas en cuanto a h
pero no en cuanto a g,
que suele escribirse:
El sistema (63.6) se
resuelve por aproximaciones sucesivas.
Llamemos
y hallemos:
Deduciremos ![]() de (65.6),
haciendo:
de (65.6),
haciendo:
![]()
y derivando respecto a g los dos miembros de la igualdad:
![]()
de donde:
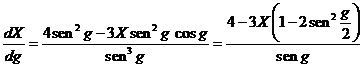
es decir:
Para calcular ![]() haremos
haremos
![]()
de donde
Sustituyendo, pues, (67.6) y
(68.6) en (66.6), obtendremos:
Todavía podemos expresar ![]() en función de x:
en función de x:
De (64.6) obtenemos:
![]()
de donde:
![]()
y sustituyendo dicho valor en (69.6),
obtenemos finalmente:
Para integrar la ecuación diferencial (70.6) procederemos por desarrollo en serie, para lo cual
escribiremos:
y derivando respecto a x:
Sustituyendo (71.6) y (72.6) en (70.6), tendremos:
Identificando coeficientes en (73.6) obtendremos:
![]()
y sustituyendo en (71.6):
![]()
El desarrollo de ![]() converge más
rápidamente que el de X, por cuyo
motivo se utiliza
converge más
rápidamente que el de X, por cuyo
motivo se utiliza
![]()
o lo que es lo mismo:
![]()
con
función que se halla tabulada.
Con todo esto las ecuaciones de Gauss (63.6) se escribirán:
y eliminando x entre ellas
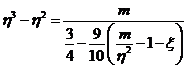
o también:
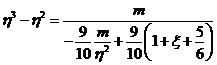
y llamando
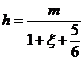
será:
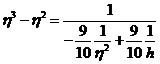
de donde, verificando operaciones, se deduce
ecuación que también se halla tabulada.
El proceso de cálculo es el siguiente:
Se toma ![]() y se calcula
y se calcula 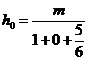
Se lleva h0 a (76.6) y se clcula h.
Calculada h, la primera ecuación del sistema (75.6) nos dará x.
Con x el desarrollo (74.6) nos dará un valor
de x con el cual calcularemos una nueva h.
Una vez obtenido h con suficiente aproximación, (64.6) nos dará g,
quedando resuelto el sistema (63.6).
Conocido el valor de g (ya conocíamos
r1, r2 y f ),
de la segunda de (58.6) se deduce a y de la primera, p, y
en consecuencia e, teniendo en cuenta
que ![]() .
.
Llevando a y g a la tercera de (57.6) deducimos G.
Recordando
que
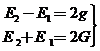
obtenemos
E1 y E2
De
la ecuación de Kepler, M1 = E1 - e sen E1,
obtenemos M1 y de M2
aplicando
M1 = n (t1- T)
obtenemos finalmente T.
6.3.6 Resumen de
fórmulas y proceso de cálculo
![]()
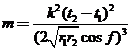
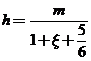 primer
valor
primer
valor ![]() à h
à h
![]() à
à ![]()
![]() à x
à x
![]() à
à ![]()
con
![]() se
vuelve a h.
se
vuelve a h.
Cuando se tiene ![]() con suficiente aproximación se hace:
con suficiente aproximación se hace:
![]()
![]() à
a
à
a
![]() à
p
à
p
p = a (1-e2) à e
r1 + r2 = 2a - 2ae cos G
cos g à ![]()
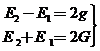 à E1 y E2
à E1 y E2
M = E – e sen E à M
M = n (t - T) à T