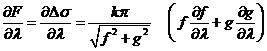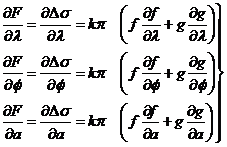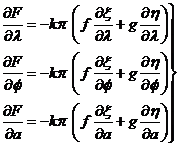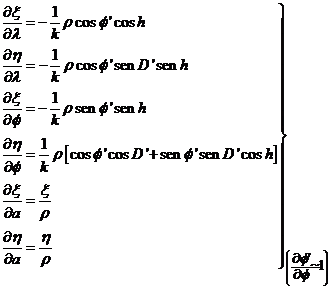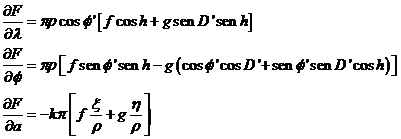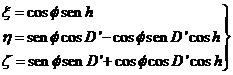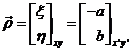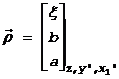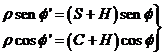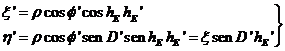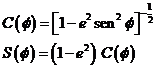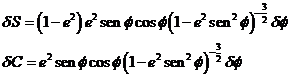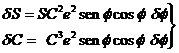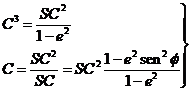10.3 Ocultaciones de estrellas por la Luna
De acuerdo con la definición de eclipse dada al principio
del capitulo, designamos por ocultación de una estrella por la Luna el fenómeno
por el cual la estrella se hace invisible al pasar aparentemente por detrás del
disco lunar.
Las fases de una ocultación son la inmersión y la emersión.
La inmersión es la desaparición de la estrella por el borde lunar y la
emersión es la reaparición de la misma. Cuando la Luna es creciente las
inmersiones se producen por el borde oscuro, que se percibe por la luz cinérea.
El observador estima el tiempo de contacto con seguridad. La reaparición por el
borde iluminado por el Sol, salvo en casos de estrellas muy brillantes, no se
aprecia. Cuando la Luna decrece las inmersiones se producen por el borde claro
y es difícil apreciarlas si no se ha calculado muy bien el ángulo de posición
correspondiente.
10.3.1 Predicción de
ocultaciones para un lugar determinado
La teoría de las ocultaciones de estrellas por la Luna es
un caso particular de la de los eclipses de Sol sustituyendo el Sol por la
estrella y tomando su paralaje y
semidiámetro iguales a
cero, con lo
cual (31.10) nos
dará f – 0º; es decir, f1
= f2 = 0º lo que
significa que en lugar de dos conos de sombra tendremos un cilindro cuyo
diámetro será el diámetro de la Luna. El punto Z (dirección del eje de dicho cilindro) será la posición de la
estrella vista desde la Luna, que coincide prácticamente con la posición de la
estrella vista desde el punto de observación a causa de la gran distancia que
nos separa de ella. Evidentemente en un lugar de la Tierra habrá ocultación si
la distancia de dicho lugar al eje del cono de sombra es menor que el radio de
sombra.
La
posición de Z vendrá dada, por tanto,
por
a = A d
= D
d
= D
siendo (A , D
, D ) las coordenadas ecuatoriales de la estrella, y además, el
radio del cilindro sera
) las coordenadas ecuatoriales de la estrella, y además, el
radio del cilindro sera
L = l = RL (radio medio de la Luna)
Las
coordenadas de la Luna obtenidas en (20.10)
seran:
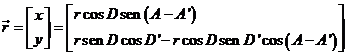 (81.10)
(81.10)
siendo
r = 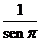 si se toma como unidad
el radio de la Tierra y r =
si se toma como unidad
el radio de la Tierra y r = 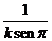 si tomamos como unidad
el radio de la Luna (k = RL / RT ).
si tomamos como unidad
el radio de la Luna (k = RL / RT ).
Sustituyendo
este último valor de r en (81.10) obtenemos:
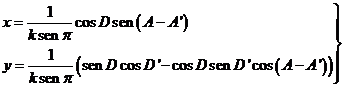 (82. 10)
(82. 10)
Si hacemos cos (A
- A ) = [1 - sen2 (A - A
) = [1 - sen2 (A - A )]½ ≈ 1 -
)]½ ≈ 1 - 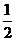 sen2
(A - A
sen2
(A - A ) y sustituimos en (82.10) nos queda
) y sustituimos en (82.10) nos queda
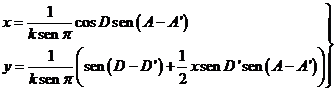 (83.10)
(83.10)
Las
expresiones (83.10) pueden escribirse en forma
aproximada haciendo
k sen π = 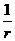 = sen s = s
= sen s = s
y
sen (A - A ) = A - A
) = A - A
quedando
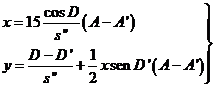 (84.10)
(84.10)
El hecho de que en la expresión de x aparezca el factor 15 es debido a que el semidiámetro
s se da en segundos de arco y la diferencia de
ascensiones rectas A - A en segundos de tiempo.
en segundos de tiempo.
Las
expresiones (84.10) se utilizan para la predicción de
las ocultaciones.
10.3.2 Epocas y ángulos de posición
de la inmersión y la emersión para un lugar determinado
Las
coordenadas del observador (23.10) en unidades
del radio de la Luna seran:
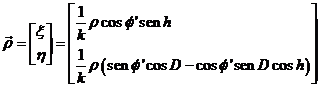 (85. 10)
(85. 10)
siendo h el ángulo horario de la estrella.
|
|
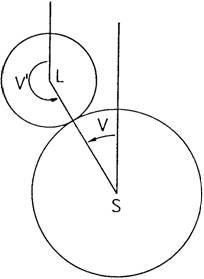
Los ángulos de posición que contábamos
sobre el Sol ahora deberán contarse sobre la Luna lo cual implica sumar 180º
a los valores obtenidos en la teoría de eclipse de Sol (Fig.
24.10):
|
|
|
V = V + 180º = V + 180º
χ = P + 180º (86.10)
|
|
|
La distancia 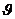 del observador al
eje del cilindro de sombra es igual a la distancia del punto O del observador al
eje del cilindro de sombra es igual a la distancia del punto O , proyección ortogonal de la posición del observador
sobre el plano fundamental, al punto L , proyección ortogonal de la posición del observador
sobre el plano fundamental, al punto L
|
|
|
FIG. 24.10
|
|
intersección
del eje de sombra con dicho plano (Fig.8.l0). Es
decir:
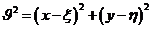 (87. 10)
(87. 10)
Pero,
en la teoría de ocultaciones es
x – ξ = f y – η = g
de donde
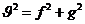 (88.10)
(88.10)
En el instante de la inmersión, suponiendo la Luna
esférica, la posición del observador correcta y las efemérides correctas, es 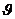 = RL y tomando
el radio de la Luna como unidad (RL
= 1), tenemos:
= RL y tomando
el radio de la Luna como unidad (RL
= 1), tenemos:
f2 + g2 = 1 (89.10)
y según (86.10)
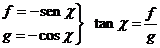 (90.10)
(90.10)
Para calcular las épocas de los contactos (inmersión y
emersión) llamemos T0 a
una época aproximada de la ocultación, que puede ser el instante de la
conjunción en ascensión recta de la Luna con la estrella deducido de las
efemérides de la Luna, y τ la
diferencia entre esta época y la real Tc
(seguimos de momento suponiendo la Luna esférica). Se verifica:
Tc = T0 + τ (91.10)
Si (x , y
, y ), (ξ
), (ξ , η
, η ) son las variaciones horarias de las dos primeras
coordenadas besselianas (x, y), (ξ,
η) de la Luna y del observador
respectivamente en la época T0,
las coordenadas en la época Tc
(91.10) serán:
) son las variaciones horarias de las dos primeras
coordenadas besselianas (x, y), (ξ,
η) de la Luna y del observador
respectivamente en la época T0,
las coordenadas en la época Tc
(91.10) serán:
(x + x τ, y + y
τ, y + y τ)
y (ξ + ξ
τ)
y (ξ + ξ τ, η + η
τ, η + η τ) (92.10)
τ) (92.10)
x e y
e y se calculan tal como hemos explicado para el caso de un
eclipse de Sol (10.1.5). Para calcular ξ
se calculan tal como hemos explicado para el caso de un
eclipse de Sol (10.1.5). Para calcular ξ y
η
y
η derivaremos las expresiones de ξ y η dadas en
(85.10) suponiendo nula la variación de la declinación
de la estrella. Obtendremos:
derivaremos las expresiones de ξ y η dadas en
(85.10) suponiendo nula la variación de la declinación
de la estrella. Obtendremos:
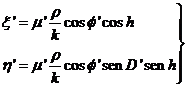 (93.
10)
(93.
10)
donde μ
- λ = (θ
- A ) = h y por tanto μ
) = h y por tanto μ = h
= h
Tomando
h =
= 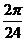 1.00273791 = 0.262516
1.00273791 = 0.262516
podremos escribir (93.10) en la forma:
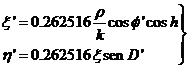 (94.10)
(94.10)
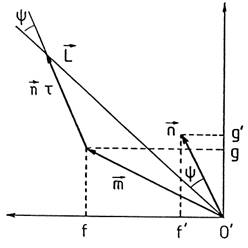
Consideremos ahora
los vectores (Fig.25.10):
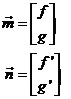
Para la época
Tc = T + τ tenemos:
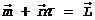
FIG. 25.10
Aplicando
aquí la (46.10) obtenemos
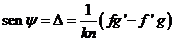 (95.10)
(95.10)
con 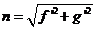 . Al igual que en la teoría de eclipses el ángulo ψ queda indeterminado.
. Al igual que en la teoría de eclipses el ángulo ψ queda indeterminado.
De
(48.10) deducimos
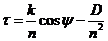 (96.10)
(96.10)
con D = f f  + g g
+ g g , tomándose cos ψ
>O para las emersiones y cos ψ
< O para las inmersiones. Habremos obtenido pues Tci = T0
+ τi, Tce = T0
+ τe. Como en el
cálculo de las circunstancias de un eclipse de Sol, para una segunda
aproximación se calcularán las épocas de inmersión y emersión por separado a
partir de las épocas aproximadas anteriormente obtenidas.
, tomándose cos ψ
>O para las emersiones y cos ψ
< O para las inmersiones. Habremos obtenido pues Tci = T0
+ τi, Tce = T0
+ τe. Como en el
cálculo de las circunstancias de un eclipse de Sol, para una segunda
aproximación se calcularán las épocas de inmersión y emersión por separado a
partir de las épocas aproximadas anteriormente obtenidas.
10.3.3 Reducción de
observaciones
La información que nos da una ocultación proporciona una
relación entre la posición de la estrella, el limbo lunar y la posición del
observador en el instante de la ocultación. Puede hacerse una reducción
adecuada para eliminar el efecto de la posición del observador, hallando el
exceso de distancia aparente de la estrella al centro de la Luna respecto al
valor tomado del semidiámetro de la Luna supuesta esférica
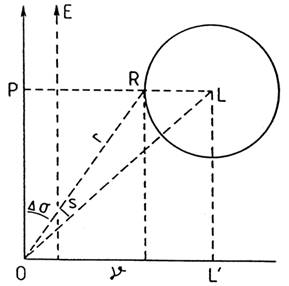
FIG 26.10
Sean L el centro
de la Luna, P la posición aparente de
la estrella y O la posición del observador en un instante dado. Sea además
Δσ la distancia angular aparente de la estrella al limbo lunar
(Fig. 26.10). En dicho instante, la proyección sobre el
plano fundamental de la distancia del observador al centro de la Luna según (87.10) es
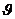 = [(x - ξ)2 + (y - η)2]½
= [(x - ξ)2 + (y - η)2]½
La proyección de la distancia del observador al limbo
lunar, tomando el radio de la Luna como unidad, será, por consiguiente
PR = [(x - ξ)2 + (y - η)2]
½ - 1
(97.10)
que corresponde a la
distancia angular Δσ.
Para
hallar dicha distancia angular, dada la pequeñez de los ángulos, según la misma
figura 26.10 podemos escribir:
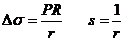
y por tanto, según (97.10)
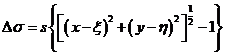 (98.10)
(98.10)
pero
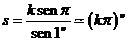
y por consiguiente:
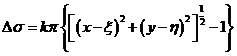
y recordando el
significado de f y g (f
= x – ξ, g = y
- η), queda finalmente
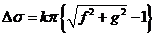 (99.
10)
(99.
10)
El proceso que se sigue para el cálculo del tiempo real de
la ocultación, suponiendo la Luna esférica, es el siguiente: A partir de una
época aproximada T0 se
obtiene un valor de Δσ y un
valor de τ que nos dará la época
Tc1 = T0
+ τ más aproximada que T0. Tomando esta época
Tc1 como inicial,
procederemos a calcular otra vez Δσ
y τ, de modo que la época de la ocultación será ahora Tc2 = Tc1 + τ1,
siendo T1 la última τ
obtenida. Cuando siguiendo este proceso iterativo lleguemos a una
Δσ nula, habremos obtenido
la época real de la ocultación, supuesta la Luna esférica. Pero, la Luna no es
una esfera perfecta pues su superficie presenta irregularidades (montañas,
valles, etc.). Mediante las tablas de Watts conocemos el relieve lunar
en el punto de contacto, en función de las libraciones en longitud y latitud
(Apartado 9.1) y del ángulo de posición del punto de contacto cuyo valor es (Fig. 27.10)
П =
χ – C (100.10)
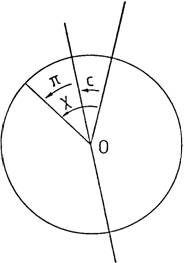
FIG. 27.10
donde
C es el ángulo de posición
topocéntrico y χ el ángulo de inmersión
o emersión con respecto al centro de la Luna medido del Norte hacia el este
(recordar 86.10).
Las cartas de Watts nos dan, en décimas de segundo de
arco, la diferencia 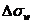 de relieve, en el
punto de contacto, entre el borde de la Luna supuesta esférica y el borde real
(Fig. 28.10).
de relieve, en el
punto de contacto, entre el borde de la Luna supuesta esférica y el borde real
(Fig. 28.10).
FIG. 28.10
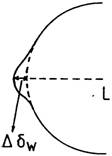 La distancia angular
La distancia angular 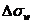 es positiva o negativa
según que la curva correspondiente en las cartas de Watts sea continua o de
trazos, lo cual indica que el borde lunar presenta una montaña o un cráter,
respectivamente.
es positiva o negativa
según que la curva correspondiente en las cartas de Watts sea continua o de
trazos, lo cual indica que el borde lunar presenta una montaña o un cráter,
respectivamente.
La distancia entre la estrella y el borde real de la Luna
será entonces
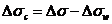
En general, 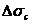 será distinto de cero,
lo cual se deberá a diversas causas:
será distinto de cero,
lo cual se deberá a diversas causas:
-
Mala determinación de la posición de la Luna (A, D, π)
-
Mala determinación de la posición del observador ( , λ, a)
, λ, a)
- Mala determinación de k
(la posición de la estrella se supone, en general, bien determinada).
Llamemos
F = 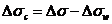 (101.10)
(101.10)
siendo
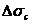 = F(A, D,
π, k,
= F(A, D,
π, k,  , λ, a) (102.10)
, λ, a) (102.10)
Teniendo
en cuenta las causas de error citadas podremos escribir:
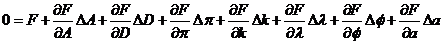 (103.
10)
(103.
10)
teniendo
para cada observación una ecuación de este tipo.
Como que las incógnitas son siete (ΔA, ΔD, Δπ, Δk, Δ , Δλ, Δa) teóricamente nos bastarán siete
observaciones para resolver el problema. Sin embargo, en la práctica se parte
de muchas más observaciones y se resuelve el sistema de ecuaciones obtenido por
mínimos cuadrados.
, Δλ, Δa) teóricamente nos bastarán siete
observaciones para resolver el problema. Sin embargo, en la práctica se parte
de muchas más observaciones y se resuelve el sistema de ecuaciones obtenido por
mínimos cuadrados.
Para simplificar el cálculo se suele suponer que no hay
error en la determinación de la posición de la Luna con lo cual la ecuación (103.10) queda reducida a:
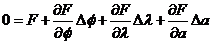 (104.
10)
(104.
10)
Para calcular los coeficientes de las incógnitas Δ , Δλ, Δa que figuran en (104.10),
tendremos en cuenta (101.10) de la que se deduce:
, Δλ, Δa que figuran en (104.10),
tendremos en cuenta (101.10) de la que se deduce:
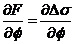
y análogamente para
las demás derivadas.
Así pues, partiendo de (99.10) y
derivando respecto a λ,  y a, obtendremos:
y a, obtendremos:
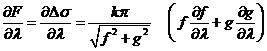 (105.10)
(105.10)
y
teniendo en cuenta que 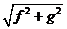 = 1 y generalizando a las otras variables, podemos escribir:
= 1 y generalizando a las otras variables, podemos escribir:
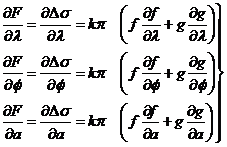 (106.10)
(106.10)
Ahora bien, teniendo en cuenta que f = x - ξ y g = y - η, y que x e y no dependen de
(λ,  , a)
obtendremos a partir de las expresiones (106.10):
, a)
obtendremos a partir de las expresiones (106.10):
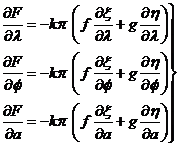 (107.10)
(107.10)
Derivando respecto a λ,  y a las expresiones (85.10) obtenemos:
y a las expresiones (85.10) obtenemos:
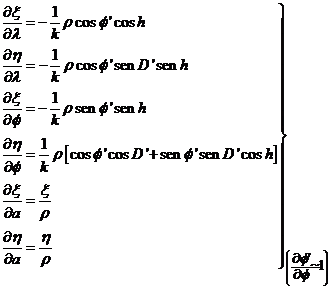 (108.10)
(108.10)
y sustituyendo en las
(107.10):
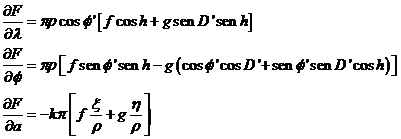 (109.10)
(109.10)
con
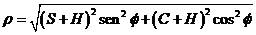
(ver
2.1.1 y 2.1.2)
Sustituyendo las expresiones (109.10)
en (104.10) tendremos para cada ocultación la ecuación:
0 = F
+ πρ [f sen 
 sen h - g(cos
sen h - g(cos

 cos D
cos D + sen
+ sen 
 sen D
sen D cos h)] Δ
cos h)] Δ +
+
πρ cos 
 (f cos h + g sen D
(f cos h + g sen D sen h) Δλ – Kπ (
sen h) Δλ – Kπ (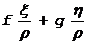 )Δa (110.10)
)Δa (110.10)
Si quisiéramos tener en
cuenta la corrección a la posición de la Luna, deberíamos añadir a la ecuación
(110.10) dos términos más: uno en ΔL y otro en ΔB que expresarían los errores en la longitud y la latitud orbitales
de la Luna.
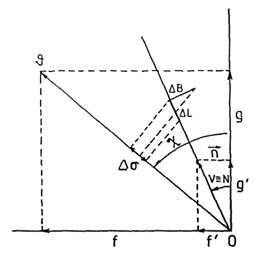
FIG.
29.10
De
la Fig. 29.10 se obtiene
Δσ = cos (χ – V) ΔL + sen (χ – V) ΔB (111.10)
con
tan V ≡≡ tan N
= 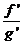
Si despreciamos el
movimiento del observador, tendremos
f  = x
= x g
g = y
= y
con lo que
tan V = 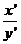
Los términos del segundo miembro de la ecuación (111.10) son los términos a añadir a la ecuación (110.10).
10.3.4 Curvas límites
Estudiaremos en este apartado la zona de la superficie
terrestre desde la cual es visible una determinada ocultación, hallando los
paralelos de latitud que limitan dicha zona de visibilidad.
Como en el caso de los eclipses de Sol, los vectores 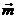 y
y 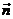 pueden expresarse por
sus componentes en la forma:
pueden expresarse por
sus componentes en la forma:
 (112.10)
(112.10)
Para un observador situado en un punto de la línea límite
que tratamos de encontrar, la distancia mínima a que se encontrará la estrella
del centro de la Luna deberá ser igual al radio de la Luna (recordemos que en
unidades del radio ecuatorial terrestre es k
= 0.2725026). En otras palabras, en la expresión (95.10)
tendremos
(x - ξ) cos N - (y - η) sen N = ± k (113.10)
Si queremos determinar los paralelos de forma aproximada
podemos despreciar las variaciones de ξ
y η frente a las de x e y,
con lo que el valor de N vendrá dado
por
tan
N = 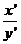 (114.10)
(114.10)
Si llamamos x0
e y0 a los valores de x e y
en el instante inicial T0,
se verificará
(x0
- ξ) cos N - (y0 - η) sen N = ± k (115.10)
Por otra parte, si consideramos, para simplificar, la
Tierra esférica, las ecuaciones (23.10),
haciendo ρ = 1 y 
 =
=  se escribirán:
se escribirán:
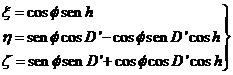 (116.10)
(116.10)
donde
ξ, η, ζ vienen
expresadas en radios terrestres.
Si multiplicamos la segunda de (116.10)
por cos D , la tercera por sen D
, la tercera por sen D y sumamos, obtenemos
y sumamos, obtenemos
sen  = η cos D
= η cos D + ζ sen D
+ ζ sen D (117.10)
(117.10)
cumpliéndose
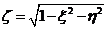
Hallaremos
los paralelos límites de latitud buscando los valores máximo y mínimo de la latitud
en (117.10) que verifiquen (115.10).
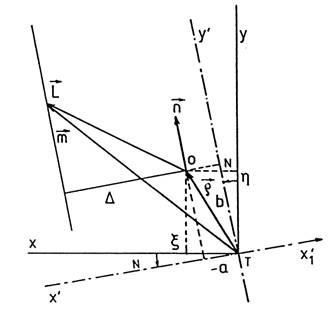
FIG. 30.10
Para ello introduciremos un cambio de ejes de coordenadas
(Fig. 30.10). Tomaremos como nuevo eje y (que llamaremos y ) la
dirección del movimiento relativo de la Luna y el observador, o sea la
dirección de
) la
dirección del movimiento relativo de la Luna y el observador, o sea la
dirección de 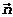 . Llamemos -a y
b a las componentes de
. Llamemos -a y
b a las componentes de 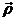 en esta nueva
base:
en esta nueva
base:
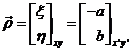 (118.
10)
(118.
10)
Para pasar de la base x , y
, y a la x, y
aplicaremos la matriz R3(N) con lo cual
a la x, y
aplicaremos la matriz R3(N) con lo cual
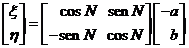
es decir:
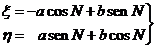 (119.
10)
(119.
10)
verificándose
ζ2 + a2 + b2 = 1 (120.10)
Desarrollando
(115.10) y utilizando las (119.10)
obtenemos:
x0 cos N
- y0 sen N + a = ± k
o sea:
a = - x0 cos N + y0 sen N ± k
(121.10)
que en nuestra
hipótesis es constante.
Consideremos
ahora la base z, y , x
, x l con x
l con x 1, opuesta a x
1, opuesta a x e y
e y y z los mismos ejes de antes (Fig. 31.10). Tomemos
los elementos auxiliares γ
y є definidos por
y z los mismos ejes de antes (Fig. 31.10). Tomemos
los elementos auxiliares γ
y є definidos por
a = cos γ
b = sen γ cos є (122.10)
ζ = sen
γ sen є
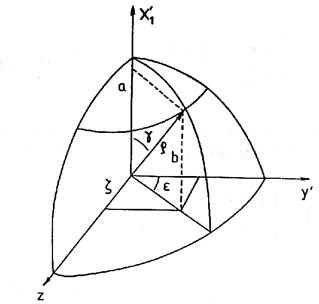
FIG. 31.10
Las componentes en esta base del vector de posición 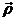 del observador
son:
del observador
son:
|
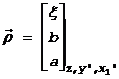
|
(123.10)
|
y las coordenadas
esféricas del observador son (є, γ) con sen γ > 0 (ver Fig. 31.10).
Sustituyendo
en (117.10) la expresión de η de (119.10), obtenemos
sen  = (a sen N + b cos N) cos D
= (a sen N + b cos N) cos D + ξ sen D
+ ξ sen D (124.10)
(124.10)
y utilizando (122.10)
sen  = cos γ sen N cos D
= cos γ sen N cos D + sen γ cos є cos N cos D
+ sen γ cos є cos N cos D + sen γ sen є sen D
+ sen γ sen є sen D (125.10)
(125.10)
e
introduciendo ahora los ángulos auxiliares β y λ (Fig. 32.10) definidos por
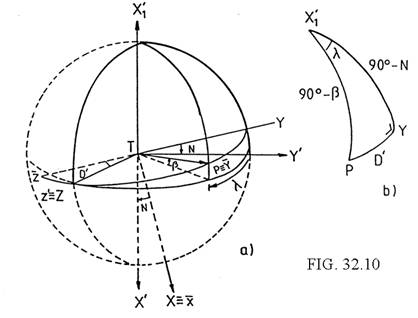
sen N cos D =
sen β
=
sen β
cos N cos D = cos β cos λ
= cos β cos λ
sen D =
cos β sen λ (126.10)
=
cos β sen λ (126.10)
con cos β siempre positivo, sustituyendo (126.10) en (125.10), resulta
sen  = sen β cos γ + cos β sen γ cos (λ - є) (127.10)
= sen β cos γ + cos β sen γ cos (λ - є) (127.10)
Para ver el significado de los ángulos β y λ supongamos
que en la figura 32.10 P
es el polo norte terrestre y el plano determinado por 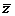 y
y 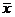 es el plano
ecuatorial. Es fácil ver que dichos ángulos representan una longitud y una
latitud de P. En efecto, aplicando al
triángulo esférico P Y X
’1 (Fig. 32.l0,b) rectángulo en Y las fórmulas de la trigonometría
esférica, se obtienen sin dificultad las expresiones (126.10).
es el plano
ecuatorial. Es fácil ver que dichos ángulos representan una longitud y una
latitud de P. En efecto, aplicando al
triángulo esférico P Y X
’1 (Fig. 32.l0,b) rectángulo en Y las fórmulas de la trigonometría
esférica, se obtienen sin dificultad las expresiones (126.10).
En (127.10)
obtendremos el valor
máximo de  cuando sea
cos (λ -є) = 1 o sea cuando λ = є en cuyo caso
cuando sea
cos (λ -є) = 1 o sea cuando λ = є en cuyo caso
sen  M = sen (β
+ γ)
M = sen (β
+ γ)
y
obtendremos el valor mínimo de  cuando cos (λ - є) = - 1 o sea
λ - є =
180º, con lo cual
cuando cos (λ - є) = - 1 o sea
λ - є =
180º, con lo cual
sen  m = sen (β
- γ)
m = sen (β
- γ)
Es decir, el límite
norte vendrá determinado por
 = β + γ (128.10)
= β + γ (128.10)
y el límite sur por
 = β - γ
(129.10)
= β - γ
(129.10)
Puesto que de los dos valores opuestos que puede tomar ζ sólo nos interesa el positivo
(para el cual la ocultación es visible), según (122.10),
tomándose sen γ positivo deberá serlo también sen є. Para el límite norte: λ = є
y sen λ > 0, y, según (126.10) sen D > 0, luego D
> 0, luego D > O (pues cos β > 0).
> O (pues cos β > 0).
La expresión (128.10) nos da, pues,
el límite norte de visibilidad sólo cuando la declinación de la estrella es
positiva (D > 0).
> 0).
Para el límite sur, análogamente, la expresión (129.10) da el límite sur de visibilidad sólo cuando la declinación
de la estrella es negativa (D < 0).
< 0).
Para cada uno de los dos casos el segundo límite de
visibilidad será, evidentemente, uno de los dos puntos en los cuales las curvas
límites generales norte y sur tocan a las curvas límites correspondientes al orto y ocaso, puntos en los cuales ζ = 0 y, por tanto, sen є = 0, cos є
± 1 que reducen la fórmula
(125.10) a
sen  = sen (N ± γ) cos D
= sen (N ± γ) cos D
Si cos N es
positivo, el signo superior de esta ecuación nos dará el límite norte para el
caso en que la declinación de la estrella sea negativa y el signo inferior nos
dará el límite sur para estrellas de declinación positiva. Recíprocamente, si
cos N es negativo, el signo superior
nos dará el límite sur para declinaciones positivas y el inferior nos dará el
límite norte para declinaciones negativas.
10.3.5 Ocultaciones rasantes
Cuando
en una ocultación de una estrella por la Luna el tiempo transcurrido entre la
inmersión y la emersión estelar es inferior a 10 minutos, hecho que se produce
si la estrella se oculta por una zona próxima a los polos norte o sur lunares,
se dice entonces que la ocultación es rasante. En este caso, puede ocurrir que el fenómeno conste de
varias inmersiones y varias emersiones debidas al relieve lunar en dicha zona.
Una ocultación rasante puede ser observada, en principio,
desde un punto situado sobre los paralelos de latitud límites ya que desde
tales puntos la trayectoria aparente de la estrella se observa tangente al
limbo lunar. En todo caso, dicho fenómeno será visible a lo largo de una línea,
denominada línea límite (norte o sur)
que, debido a la variación de la declinación de la Luna, no coincidirá con el
paralelo de latitud límite (norte o sur).
Recordemos que en el apartado anterior los paralelos
límites han sido calculados en forma aproximada suponiendo la Tierra esférica.
En el caso que nos ocupa deberemos calcular con precisión la posición de la
línea límite, lugar geométrico de los puntos de la superficie terrestre desde
los cuales se observa la trayectoria de la estrella tangente al limbo medio
lunar. Para ello, partiremos del valor aproximado de la latitud máxima o mínima
(según se quiera calcular la línea límite norte o sur) obtenida en 10.3.4 y calcularemos, para una longitud geodésica determinada,
el valor exacto de la latitud de la línea límite.
Como en el cálculo de una ocultación normal (llamada
también ocultación total en
contraposición a la rasante) tomaremos como tiempo inicial aproximado el tiempo
T0 de conjunción en
ascensión recta de la estrella con el
centro de la Luna. Para este instante inicial, calcularemos las coordenadas
besselianas (x, y) del centro de la Luna en unidades del radio ecuatorial terrestre
(81.10) y el ángulo horario hE = θ +
A de la estrella a
partir de
de la estrella a
partir de
hE = θ0
+ 1.00273791 T0 – λ - A
siendo
θ0 el tiempo sidéreo
en Greenwich a 0h de T.U.
Las coordenadas del observador (ξ,
η) se obtendrán de las ecuaciones (85.10)
pero tomando como unidad el radio ecuatorial terrestre. Los valores de ρ sen 
 y ρ
cos
y ρ
cos 
 vendrán dados
por las fórmulas
vendrán dados
por las fórmulas
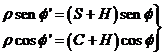 (130.10)
(130.10)
donde
S y C son funciones de la latitud astronómica y H la altitud reducida del lugar (ver apartado 2.1.1). Haciendo H = 0 se obtendrá la curva límite al
nivel del mar.
Las variaciones horarias x e y
e y de las coordenadas x
e y de la Luna se calculan con
suficiente precisión hallando
los valores de dichas coordenadas lunares para los
instantes T0 + 10m y T0 – 10m y
multiplicando por 3 la diferencia entre los mismos. Los valores de x
de las coordenadas x
e y de la Luna se calculan con
suficiente precisión hallando
los valores de dichas coordenadas lunares para los
instantes T0 + 10m y T0 – 10m y
multiplicando por 3 la diferencia entre los mismos. Los valores de x e y
e y se toman como constantes en todo el proceso de cálculo.
se toman como constantes en todo el proceso de cálculo.
Las variaciones horarias ξ y η
y η de las coordenadas ξ y η del observador se obtienen
derivando respecto al tiempo las relaciones (85.10)
expresadas en radios ecuatoriales terrestres:
de las coordenadas ξ y η del observador se obtienen
derivando respecto al tiempo las relaciones (85.10)
expresadas en radios ecuatoriales terrestres:
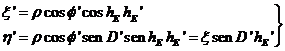 (131.10)
(131.10)
donde hE es la variación horaria de la estrella que, en radianes por
hora vale
es la variación horaria de la estrella que, en radianes por
hora vale
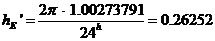
Introduciendo los elementos auxiliares f, g, f  , g
, g que hemos utilizado anteriormente, la fórmula (95.10) nos proporciona el valor de sen ψ = Δ que
representa la mínima distancia entre la trayectoria aparente del centro de la
Luna y el observador, tomando como unidad el radio de la Luna.
que hemos utilizado anteriormente, la fórmula (95.10) nos proporciona el valor de sen ψ = Δ que
representa la mínima distancia entre la trayectoria aparente del centro de la
Luna y el observador, tomando como unidad el radio de la Luna.
Esta distancia Δ
deberá ser igual al radio de la Luna (unidad en este caso) para que
en el lugar de latitud  , la ocultación sea rasante, es decir, la trayectoria aparente
de la estrella sea tangente al limbo medio de la Luna. Si no fuera así (Δ
≠ 1), deberíamos efectuar la corrección correspondiente a la
latitud del punto de observación. Dicho de otro modo, deberíamos conocer la
variación de Δ con
, la ocultación sea rasante, es decir, la trayectoria aparente
de la estrella sea tangente al limbo medio de la Luna. Si no fuera así (Δ
≠ 1), deberíamos efectuar la corrección correspondiente a la
latitud del punto de observación. Dicho de otro modo, deberíamos conocer la
variación de Δ con  .
.
En general, la variación de Δ con respecto a la posición del observador será
debida a variaciones en la longitud, la latitud y la altitud del punto de
observación.
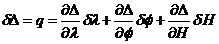
En nuestro caso tomamos una longitud dada, constante, y
calculamos la curva límite para H = 0. Por tanto,
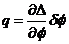 (132.10)
(132.10)
Como que los elementos besselianos son independientes de
la posición del observador, se cumple:
δf = - δξ
δg = - δη (133.10)
Por otra parte, teniendo en cuenta que las funciones S y C
se pueden escribir en la forma (ver (7.2) y (8.2)):
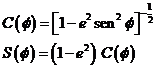 (134. 10)
(134. 10)
derivándolas con
respecto a  se obtiene
se obtiene
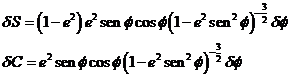
que se puede escribir
también de la forma:
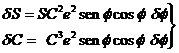 (135. 10)
(135. 10)
Teniendo
en cuenta (130.10) y que H = 0 es
ξ = C cos  sen hE
sen hE
y por tanto, serà:
δξ = -C sen sen hE δ
sen hE δ + cos
+ cos sen hE
δC
sen hE
δC
o sea
δξ = (C3
e2 cos2  - C) sen
- C) sen  sen hE δ
sen hE δ (136.
10)
(136.
10)
De
(134.10) se deduce:
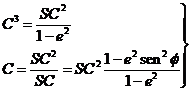 (137.10)
(137.10)
Sustituyendo
en (136.10) se obtiene finalmente
δξ = -SC2
sen  sen hE δ
sen hE δ (138.10)
(138.10)
De η = S
sen  cos D
cos D - C cos
- C cos  sen D
sen D cos hE
cos hE
escrita
teniendo en cuenta otra vez (130.10), se deduce
δ
η = sen  cos D
cos D δS + S
cos
δS + S
cos  cos D
cos D δ
δ - cos
- cos  sen D
sen D cos hE δC +
cos hE δC +
+ C sen  sen D
sen D cos hE δ
cos hE δ
y sustituyendo los
valores encontrados de δS y δC:
δ
η = (S
C2 e2 sen2 + S) cos
+ S) cos  cos D
cos D δ
δ +
+
+ (C
– C3 e2 cos2 ) sen
) sen  sen D
sen D cos hE δ
cos hE δ (139.10)
(139.10)
Sustituyendo (137.10)
en (139.10) y haciendo
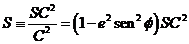
resulta:
δ η = SC2 (cos  cos D
cos D + sen
+ sen  sen D
sen D cos hE)
δ
cos hE)
δ (140.10)
(140.10)
Derivando
la fórmula (95.10) respecto a  tendremos:
tendremos:
δΔ = q = 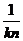 (g
(g δf – f
δf – f  δg) δ
δg) δ =
= 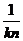 (f
(f  δη - g
δη - g δξ) δ
δξ) δ (141.10)
(141.10)
y sustituyendo (138.10) y (140.10) en esta última:
q = 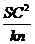 [f
[f  (cos
(cos  cos D
cos D + sen
+ sen  sen D
sen D cos hE) + g
cos hE) + g sen
sen  sen hE]
δ
sen hE]
δ (142. 10)
(142. 10)
fórmula
que proporciona la variación de Δ con la latitud. Si hacemos δ = lº, obtendremos la
variación de Δ por grado de variación de
= lº, obtendremos la
variación de Δ por grado de variación de  .
.
La
corrección que deberá hacerse a la latitud será entonces
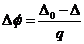 (143.10)
(143.10)
donde Δ0
= 1 si buscamos el límite norte y Δ0 = -1 si buscamos el limite sur. En
efecto, si se trata de un límite norte, Δ
= sen ψ es positivo y
por tanto 1 - Δ representa la máxima distancia de la estrella al limbo
lunar norte; luego dividiendo esta máxima distancia por la variación q de Δ con la latitud, tendremos
efectivamente la corrección a aplicar a  . Si,
en cambio, se trata de un límite sur, Δ es negativo y (-1 - Δ) representará asimismo la
máxima distancia de la estrella al limbo lunar sur y, como antes, al dividirlo
por q tendremos cómo debe variar
. Si,
en cambio, se trata de un límite sur, Δ es negativo y (-1 - Δ) representará asimismo la
máxima distancia de la estrella al limbo lunar sur y, como antes, al dividirlo
por q tendremos cómo debe variar  para que desde el
nuevo punto se vea la trayectoria de la etrella tangente a dicho limbo.
para que desde el
nuevo punto se vea la trayectoria de la etrella tangente a dicho limbo.
En cuanto a la variación en el tiempo, utilizaremos la
expresión (96.10) que escribiremos en la forma
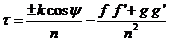 (144.10)
(144.10)
Pero,
en las proximidades del punto de contacto de una ocultación rasante, el ángulo ψ
es aproximadamente igual a 90º, por lo que puede despreciarse
el primer término de (144.10) y tomar simplemente
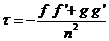
Con los nuevos valores encontrados de la latitud ( + Δ
+ Δ ) y
del tiempo (T0 + τ) puede
repetirse el proceso tomando dichos valores como aproximados, llegándose a
valores más exactos de
) y
del tiempo (T0 + τ) puede
repetirse el proceso tomando dichos valores como aproximados, llegándose a
valores más exactos de  y T.
y T.
El ángulo de posición χ del punto en que se produce
la ocultación rasante se calcula, una vez efectuada la última iteración,
mediante la fórmula (90.10).
Una vez efectuado el cálculo de la latitud que corresponde
a una cierta longitud λ, se repiten los cálculos para
longitudes distintas de la anterior obteniendo sucesivamente los distintos
puntos de la línea límite (al nivel del mar).
10.3.6 Observación de
ocultaciones rasantes
Cuando uno de los paralelos de latitud que limitan la zona
desde la que es visible una ocultación de una estrella por la Luna pasa cerca
de nuestra estación, se procede al cálculo preciso de la posición de la línea
límite desde la cual la ocultación será rasante.
Una de las ventajas de la observación de ocultaciones
rasantes es que puede ser efectuada con telescopios de poca abertura. Ello, no
obstante, obliga a una serie de restricciones a la hora de realizar una
observación. Por ejemplo, debe tenerse en cuenta la magnitud de la estrella y,
sobre todo, si la ocultación se produce por el borde oscuro o el iluminado de
la Luna, para lo cual debe calcularse el ángulo de posición del cuerno
iluminado y compararlo con el ángulo de posición de la rasante, teniendo en
cuenta la fase de la Luna (creciente o decreciente).
Una vez efectuada la predicción se procede a representar
sobre un mapa, a la mayor escala posible, los distintos puntos de la línea
límite, que, como hemos dicho, está calculada para el nivel del mar. En
consecuencia, deberá corregirse para obtenerla sobre la superficie topográfica.
Para ello se ve que (Fig. 33.10) en un lugar A, al nivel del mar, se observa el mismo
fenómeno que en el lugar B, de
altitud a. Por lo tanto, la línea
límite habrá que desplazarla en la dirección del acimut de la Luna una
distancia
b = a cot h
donde
h es la altura de la estrella (o de
la Luna).
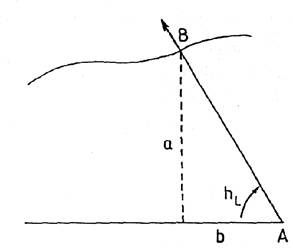
FIG. 33.10
Hecho esto, se procede a trazar el perfil previsto de la
zona desde la que se observa la ocultación, utilizando para ello la obra “The
Marginal Zone of the Moon” de C.B. Watts (llamada cartas de Watts). Con este
fin se calcula el ángulo de posición П
del punto del limbo lunar por el que empieza la ocultación referido
al eje de rotación de la Luna, a partir de los datos que proporcionan los
Anuarios de las libraciones geocéntricas en longitud l0 y en latitud b0
y del ángulo de posición C0,
o bien por cálculo directo empleando las fórmulas que hemos visto en los
apartados anteriores.
A partir de l0, b0 y C0 se calculan l, b
y C (valores topocéntricos)
utilizando las expresiones dadas en 9.1.3. El ángulo П se obtendrá restando C de χ (recordar (100.10).
Con los datos П, l, b se hallan las correcciones por limbo correspondientes
a ángulos de posición cada 0º.2 a partir del П hallado, que, llevados a escala conveniente como
elevaciones o depresiones (respecto al limbo medio) según su signo,
proporcionan el perfil previsto de dicha zona. Normalmente
se dibujan 10º de limbo, centrados en el punto de tangencia (П) de la rasante.
Se traza el contorno del limbo medio representándolo por
un arco de cosenoide. El argumento horizontal es el ángulo de posición axial,
generalmente a escala 1º : 2.5 cm. El argumento vertical es la corrección de
limbo, ampliada a escala 1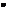 : 2.5 cm. Trazado así el limbo medio, la
trayectoria aparente de la estrella será una línea recta tangente al limbo
lunar.
: 2.5 cm. Trazado así el limbo medio, la
trayectoria aparente de la estrella será una línea recta tangente al limbo
lunar.
La observación de una ocultación rasante adquiere
importancia cuando se dispone de varios equipos establecidos a distintas
distancias de la línea límite. Según cual sea la distancia del punto de
observación a la línea límite, la trayectoria aparente de la estrella cortará
al perfil previsto a una u otra distancia de la trayectoria tangente al limbo
medio. Los puntos de observación deben elegirse teniendo en cuenta el perfil
previsto en cada caso. Para ello, se eligen sobre el mismo, las trayectorias
aparentes que se pretende ver y se mide su distancia Δ a la trayectoria tangente (en segundos de arco).
Entonces, para observar estas trayectorias, deberemos desplazarnos sobre la
línea límite, una distancia que nos vendrá determinada por el valor de q (142.10) pues
su inversa nos da la variación de latitud que deberemos efectuar
correspondiente a una variación Δ de distancia de la Luna. Si se toma esta
distancia igual a 1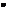 (en radios lunares rL sen 1
(en radios lunares rL sen 1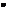 /RL) obtendremos la variación de
latitud en grados, fácilmente transformable en metros o en kilómetros.
/RL) obtendremos la variación de
latitud en grados, fácilmente transformable en metros o en kilómetros.
10.3.7 Reducción de
observaciones rasantes
Los
resultados de la observación de una ocultación rasante son únicamente los
tiempos de contacto registrados desde los distintos puntos de observacion.
Conocida la posición de los puntos de observación se
efectua la reducción de los puntos de contacto calculando para cada tiempo de
contacto el ángulo de posición χ y la separación Δσ respecto del limbo
medio (ecuaciones (90.10) y (99.10)
respectivamente). Representando los contactos como puntos sobre el limbo medio,
estos puntos deberían coincidir sobre el perfil previsto. En caso contrario,
puede estudiarse cual debe ser la corrección al ángulo de posición П o a la separación Δσw correspondiente
al perfil previsto para mejorar la coincidencia de éste con los contactos
observados.
La corrección en ángulo de posición es el llamado H.P.C.
(Horizontal Profile Correction) -bien estudiado- que nos corrige el argumento
de entrada П de las
cartas de Watts. Morrison asigna un valor promedio de -0º.25 como corrección al
ángulo de posición П de
las cartas de Watts, obtenido a partir de la observación de muchas ocultaciones
rasantes.
La corrección a la separación Δσw es el llamado V.P.C. (Vertical Profile
Correction). Este V.P.C. no tiene un valor definido, sinó que depende de la
zona de la Luna en que se produzca la ocultación rasante. La existencia de este
V.P.C. condiciona la localización de la línea límite, por lo cual se acostumbra
a incluir su efecto en las predicciones tomando para ello un V.P.C. previsto,
deducido de anteriores observaciones de ocultaciones rasantes en dicha zona de
la Luna.
Como se ve, la observación de ocultaciones rasantes sirve
para corregir las cartas de Watts. Por otra parte, por la segunda ley de
Cassini del movimiento de la Luna sabemos que hay una zona de la misma que no
es visible nunca iluminada. Por esta razón, las cartas de Watts, obtenidas a
partir de fotografia, no dan correcciones para esta zona. Las ocultaciones
rasantes producidas en dichas zonas oscuras permitirán “construir” el perfil
lunar en ellas.
A partir de la observación de gran número de observaciones
rasantes pueden determinarse ciertas fluctuaciones en el movimiento de la Luna
y establecerse las diferencias entre los patrones de tiempo (tiempo de
efemérides o dinámico y universal).
![]() d
= D
d
= D![]()
![]() , D
, D![]() ) las coordenadas ecuatoriales de la estrella, y además, el
radio del cilindro sera
) las coordenadas ecuatoriales de la estrella, y además, el
radio del cilindro sera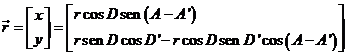 (81.10)
(81.10)![]() si se toma como unidad
el radio de la Tierra y r =
si se toma como unidad
el radio de la Tierra y r = ![]() si tomamos como unidad
el radio de la Luna (k = RL / RT ).
si tomamos como unidad
el radio de la Luna (k = RL / RT ).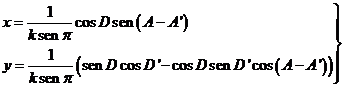 (82. 10)
(82. 10)![]() ) = [1 - sen2 (A - A
) = [1 - sen2 (A - A![]() )]½ ≈ 1 -
)]½ ≈ 1 - ![]() sen2
(A - A
sen2
(A - A![]() ) y sustituimos en (82.10) nos queda
) y sustituimos en (82.10) nos queda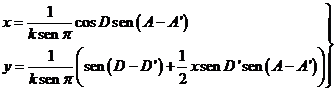 (83.10)
(83.10)![]() = sen s = s
= sen s = s![]() ) = A - A
) = A - A![]()
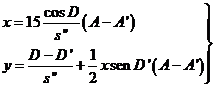 (84.10)
(84.10)![]() en segundos de tiempo.
en segundos de tiempo.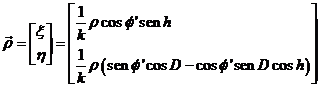 (85. 10)
(85. 10)![]() (88.10)
(88.10)![]() = RL y tomando
el radio de la Luna como unidad (RL
= 1), tenemos:
= RL y tomando
el radio de la Luna como unidad (RL
= 1), tenemos:![]() (90.10)
(90.10)![]() , y
, y![]() ), (ξ
), (ξ![]() , η
, η![]() ) son las variaciones horarias de las dos primeras
coordenadas besselianas (x, y), (ξ,
η) de la Luna y del observador
respectivamente en la época T0,
las coordenadas en la época Tc
(91.10) serán:
) son las variaciones horarias de las dos primeras
coordenadas besselianas (x, y), (ξ,
η) de la Luna y del observador
respectivamente en la época T0,
las coordenadas en la época Tc
(91.10) serán:![]() τ, y + y
τ, y + y![]() τ)
y (ξ + ξ
τ)
y (ξ + ξ![]() τ, η + η
τ, η + η![]() τ) (92.10)
τ) (92.10)![]() e y
e y![]() se calculan tal como hemos explicado para el caso de un
eclipse de Sol (10.1.5). Para calcular ξ
se calculan tal como hemos explicado para el caso de un
eclipse de Sol (10.1.5). Para calcular ξ![]() y
η
y
η![]() derivaremos las expresiones de ξ y η dadas en
(85.10) suponiendo nula la variación de la declinación
de la estrella. Obtendremos:
derivaremos las expresiones de ξ y η dadas en
(85.10) suponiendo nula la variación de la declinación
de la estrella. Obtendremos: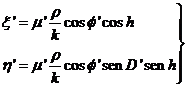 (93.
10)
(93.
10)![]() ) = h y por tanto μ
) = h y por tanto μ![]() = h
= h![]()
![]() =
= ![]() 1.00273791 = 0.262516
1.00273791 = 0.262516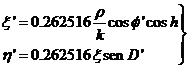 (94.10)
(94.10)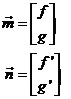
![]()
![]() . Al igual que en la teoría de eclipses el ángulo ψ queda indeterminado.
. Al igual que en la teoría de eclipses el ángulo ψ queda indeterminado.![]() (96.10)
(96.10)![]() + g g
+ g g![]() , tomándose cos ψ
>O para las emersiones y cos ψ
< O para las inmersiones. Habremos obtenido pues Tci = T0
+ τi, Tce = T0
+ τe. Como en el
cálculo de las circunstancias de un eclipse de Sol, para una segunda
aproximación se calcularán las épocas de inmersión y emersión por separado a
partir de las épocas aproximadas anteriormente obtenidas.
, tomándose cos ψ
>O para las emersiones y cos ψ
< O para las inmersiones. Habremos obtenido pues Tci = T0
+ τi, Tce = T0
+ τe. Como en el
cálculo de las circunstancias de un eclipse de Sol, para una segunda
aproximación se calcularán las épocas de inmersión y emersión por separado a
partir de las épocas aproximadas anteriormente obtenidas.![]() = [(x - ξ)2 + (y - η)2]½
= [(x - ξ)2 + (y - η)2]½![]()
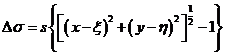 (98.10)
(98.10)![]()
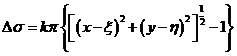
![]() (99.
10)
(99.
10)![]() de relieve, en el
punto de contacto, entre el borde de la Luna supuesta esférica y el borde real
(Fig. 28.10).
de relieve, en el
punto de contacto, entre el borde de la Luna supuesta esférica y el borde real
(Fig. 28.10). La distancia angular
La distancia angular ![]() es positiva o negativa
según que la curva correspondiente en las cartas de Watts sea continua o de
trazos, lo cual indica que el borde lunar presenta una montaña o un cráter,
respectivamente.
es positiva o negativa
según que la curva correspondiente en las cartas de Watts sea continua o de
trazos, lo cual indica que el borde lunar presenta una montaña o un cráter,
respectivamente.![]()