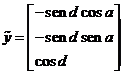10.1 Eclipses de Sol. Predicción para la Tierra en general
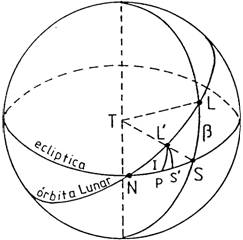
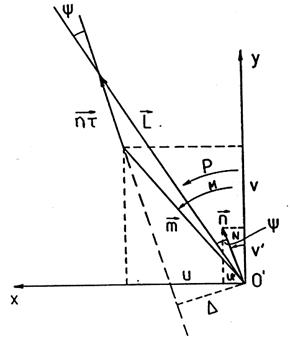
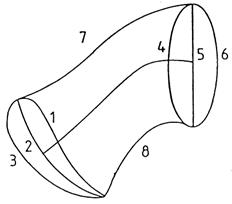
Sean (Fig. 1.10) N el nodo de la órbita lunar, I
la inclinación de dicha órbita, S y L la posición geocéntrica del Sol y la Luna
en el instante de la conjunción en longitud; S’ y L’ el Sol y la Luna
en el instante en que es mínima la distancia angular 
entre ambos; β
y β’ las latitudes de la Luna en dichos instantes; λ el cociente entre los movimientos
en longitud de la Luna y del Sol.
|
|
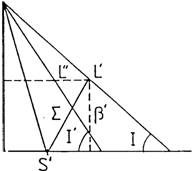
FIG. 1.10 FIG. 2.10
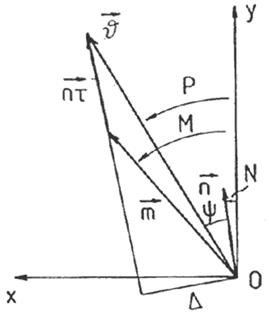
Considerando el triángulo NLS plano (Fig. 2.10), podemos escribir:
SS
= β tan γ
SP = λ β tan γ
con
de donde:
SP = SP
- SS=( λ-1) β tan γ
por otra parte:
LP = β = β-LM = β-SP tan I = β -λ β
tan γ tan I
(1.10)
Teniendo en cuenta que 
(γ varía de una configuración a otra) y haciendo d∑/dγ = 0, se obtiene para el mínimo de ∑
(2.10)
que
podemos expresar en función del movimiento relativo de la Luna
respecto al Sol. Para ello llamaremos I a la inclinación de la órbita de la Luna respecto a la
eclíptica fijando el Sol en el momento de la conjunción (S). En el triángulo L S N
de la Fig.2.l0 tenemos:
β = NS tan I
y en el triángulo L S N:
β = NS tan I
de donde:
pero
y por tanto
Sustituyendo (2.10), teniendo en cuenta (3.10) en (1.10) queda
es decir
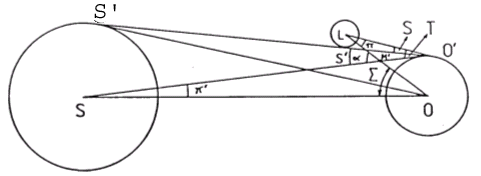
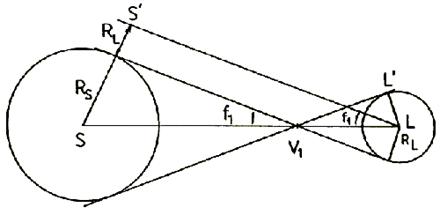
Designemos por π
y π las paralajes horizontales de la Luna y del Sol y por s y s los semidiámetros aparentes de la Luna y del Sol (Fig. 3.10).
FIG. 3.10
Entonces
T = ∑ - (π - π)
será
la distancia aparente entre los centros del Sol y de la Luna para un observador
O situado en la superficie de la Tierra. Para dicho observador
un eclipse de Sol será posible si
∑ - (π – π) < s + s
o según (4.10) si
Si en (5.10) sustituimos los valores
mínimos de π, s y s y el máximo de π (ver TABLA VIII), veremos
que el eclipse de Sol será seguro para β < 1º 24 36
Sustituyendo, en cambio, los valores máximos de π, s, s y el mínimo de π, veremos que el eclipse de Sol será imposible para β >1º 34 46, siendo dudoso entre dichos límites (para el cálculo
se ha tomado el valor medio de cos I= 
).
10.1.1 Ecuaciones
fundamentales de la teoría de eclipses
Durante
un eclipse de Sol la Luna proyectará dos conos de sombra (Fig. 4.10). Uno
tangente exterior a las superficies de la Luna y del Sol y otro tangente
interior. El primero recibe el nombre de cono de sombra y el segundo de
cono de penumbra.
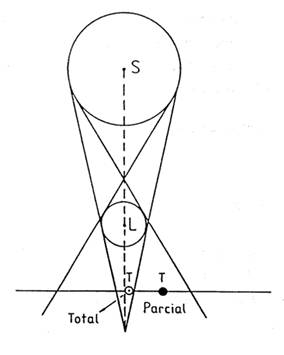
FIG 4.10
El eje de dichos conos (que une los centros de la Luna y el
Sol) es el llamado eje de sombra.
Evidentemente en un lugar de la Tierra habrá eclipse (total o parcial) si la distancia de dicho lugar al eje del cono de sombra es menor que el radio de sombra (umbral o penumbral) correspondiente a dicho lugar.
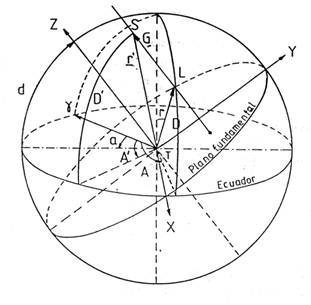
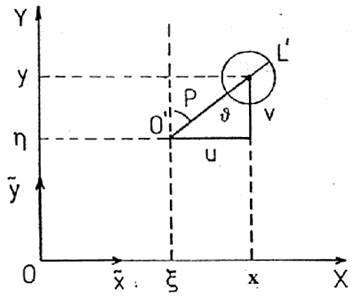
Estudiaremos las circunstancias de un eclipse de Sol para un lugar determinado. Para ello definamos un sistema de coordenadas cartesianas fundamental o de Bessel con origen en el centro de la Tierra T (Fig. 5.10), con el eje z paralelo por T al eje de sombra (positivo hacia el Sol), plano fundamental perpendicular al eje z, con el eje x intersección de dicho plano con el ecuador (positivo hacia el este) y el eje y perpendicular a x en sentido directo (positivo hacia el norte).
FIG. 5.10
Sean 
(r, A, D)
el vector de posición geocéntrico de la Luna en una base ecuatorial, 
(r, A, D) el vector de posición del Sol en la misma base y 
(G, a, d)
el vector de posición del punto Z que
define la posición del eje del cono de sombra. Las efemérides astronómicas nos
proporcionan A, D y π de la Luna (r
= 
en unidades
astronómicas, siendo П0 la
paralaje horizontal del
Sol a la
distancia media) y A, D y π del Sol (r = 
).
De la Fig. 5.10 se deduce
dividiendo
por r tenemos
y llamando
nos queda
Si escribimos la relación (6.10) tomando sus componentes ecuatoriales tendremos:
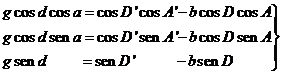
Tomando como origen de ascensiones rectas el meridiano
celeste que pasa por el Sol, lo qual equivale a efectuar una rotación de ángulo
A alrededor del eje del mundo
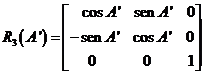
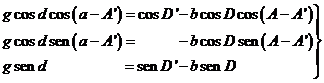(7.10)
fórmulas que permiten calcular la dirección (a, d) del eje de sombra y g.
Por otra parte para calcular b tenemos
Teniendo en cuenta los valores
las
relaciones (7.10) pueden transformarse en otras
aproximadas muy precisas. En efecto, puesto que cos D
sec D cos (A - A) 
1 dividiendo la
segunda por la primera obtendremos
o
también si suponemos cos D cos D
(8.10)
La declinación d
la podemos hallar aplicando una rotación R2(-D) a la identidad (6.10) con lo que
queda:
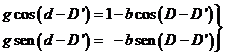(9.10)
y
dividiendo la segunda por la primera haciendo antes cos (D - D) = 1
o también
(10.10)
Luego, con mucha aproximación Z(a, d) y G vendrán definidos por las relaciones
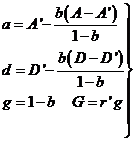(11.10)
10.1.2 Distancia al eje del cono de sombra
Consideremos en la base de Bessel los vectores unitarios 
, 
, 
(según x, y, z)
y
FIG. 6.10
hallemos
sus componentes en una base ecuatorial. Evidentemente para el vector es
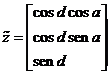(12.10)
Para hallar las componentes de supongamos un vector 
unitario en la dirección del eje del mundo. es ortogonal a y a , es decir, tiene la dirección del producto vectorial 
:
siendo λ el factor de normalización. De (13.10), tendremos, teniendo en cuenta (12.10)
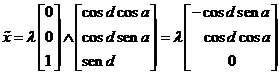(14.10)
El
módulo del vector dado por (13.10) es:
(15.10)
de donde
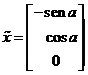(16.10)
Las componentes de las obtendremos de
sustituyendo
y 
por sus
componentes (12.10) y (16.10):
Con ello tenemos , , en función de a y d
conocidos y cualquier vector puede ahora expresarse en esta base.
Sea la posición
geocéntrica de la Luna. En la base ecuatorial geocéntrica se tiene:
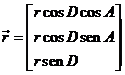(18.10)
En la base de Bessel sera:
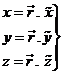(19.10)
o sea, teniendo presente (16.10), (17.10) y (12.10)
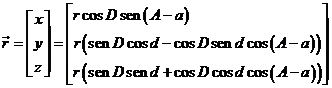(20.10)
Por otra parte, si designamos por 
y 
la latitud geocéntrica
y el radio vector correspondiente al lugar de observación y por θ el tiempo sidéreo local en él,
en la base ecuatorial sera:
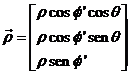(21.10)
y en la base de Bessel teniendo en cuenta que las coordenadas ξ, η, ζ del observador se obtendrán de
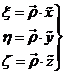(22.10)
y acudiendo otra vez a (16.10), (17.10) y (12.10), será:
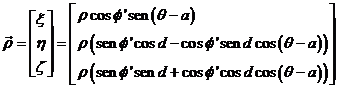(23.10)
Todo lo necesario para calcular estos vectores lo obtenemos de las “Efemérides Astronómicas”. Hay que tener en cuenta que a partir de 1985 los Anuarios publican sus efemérides astronómicas con argumento de tiempo dinámico. En las relaciones anteriores (23.10) podemos poner (Fig. 7.10)
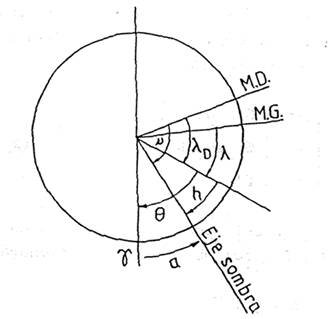siendo μ el ángulo
horario de la dirección del eje de sombra para el meridiano dinámico y λD la longitud
dinámica del lugar relacionada con la longitud geográfica por la expresión
λD = λ + 1.00274ΔT
con ΔT diferencia entre el T.D. y el T.U. (ver FIG. 7.10 apartado 4.10)
Conocidas las coordenadas rectilíneas geocéntricas (20.10) de la Luna y las del lugar de observación (23.10) en la base de Bessel, la distancia θ de dicho lugar al eje del cono de sombra vendrá dada por la relación (Fig. 8.10)
FIG. 8.10
(26.10)
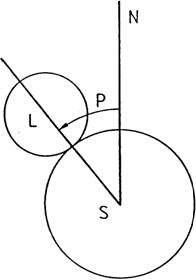y el ángulo P (Figs. 8.10 y 9.10) se obtendrá de las
relaciones
(27.10)
siendo
Más adelante (10.1.5) veremos que el valor de P nos indicará en que punto del limbo solar tiene lugar el contacto (Fig. 9.10).
FIG. 9.10
10.1.3 Radios de los conos
de sombra y penumbra
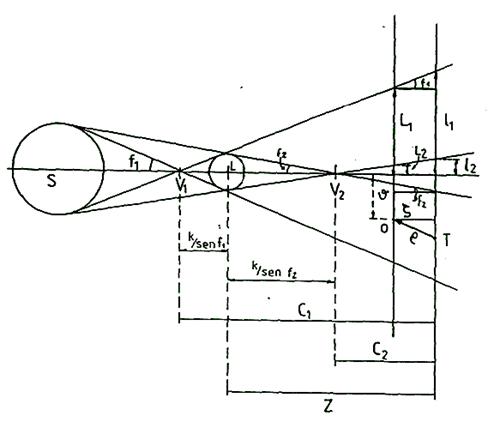
Hallaremos ahora los radios de los conos de sombra y penumbra en el plano fundamental y en el paralelo a éste por el lugar de observación. Designaremos con el subíndice 1 los elementos referentes al cono de penumbra y con el subíndice 2 los referentes al cono de sombra (Fig. 10.10).
FIG. 10.10
Sean V1
y V2 los
vértices del cono de penumbra y sombra respectivamente; f1 y f2
los ángulos de las generatrices de los conos, de penumbra y sombra, con
el eje de sombra; C1 y
C2 las
distancias de los vértices de los conos, de penumbra y sombra, respectivamente,
al plano fundamental; δ = arc
sen (k sen π0) es el semidiámetro aparente de la Luna donde π0 es la paralaje
horizontal de la Luna y k una
constante cuyo valor adoptado por la Unión Astronómica Internacional desde 1986
es k = 0.2725076 correspondiente al radio medio de
la Luna tomando el ecuatorial de la Tierra como unidad, y H = 959,63 el semidiámetro aparente del Sol.
De la Fig. 10.10 se deduce:
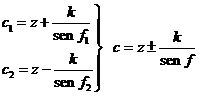(28.10)
Los ángulos f1 y f2 se hallan en los anuarios.
FIG. 11.10
De la Fig. 11.10 por semejanza de triángulos podemos obtener
y
recordando que G = g r:
Análogamente, para f2:
Las expresiones (29.10) y (30.10) suelen escribirse, agrupándolas, como:
En la misma figura 10.10 llamemos l al radio de los conos de sombra sobre el plano fundamental (l1 radio del cono de penumbra, l2 radio del cono de sombra) y L al radio de los conos sobre el plano paralelo al plano fundamental que pasa por el observador (Ll del cono de penumbra y L2 del de sombra). Se deduce:
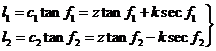(32.10)
o también, agrupando:
(33.10)
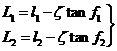(34.10)
o
(35.10)
10.1.4 Circunstancias de un eclipse para un lugar determinado
Antes del cálculo de las circunstancias de un eclipse para
un lugar determinado observemos que las variaciones horarias x, y y l de las coor denadas x,
y y l se obtienen a partir de las diferencias entre los valores que
figuran en las tablas de elementos generales o besselianos que se publican en
los anuarios. Para calcular las variaciones horarias de ξ y η tendremos
que derivar sus expresiones dadas en (23.10), quedando
al tener en cuenta (24.10):
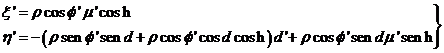
o también:
(36.10)
Para
los valores 
y 
se toman sus
variaciones horarias.
a) Principio y fin del eclipse
Observando una vez más la Fig. 10.10 deducimos:
Si
= L1 comienza o acaba un eclipse parcial
Si
= L2 pueden suceder dos casos:
a) ζ > c2 habrá
eclipse total
b) ζ < c2 habrá tangencia interior
Podemos por tanto escribir que la condición general de principio y fin del eclipse será:
De las ecuaciones (25.10) y (26.10) deducimos, por tanto:
(38.10)
En el entorno del tiempo en que esto se verifica, tomemos un tiempo T0 y sean x, y, ξ, η, las coordenadas de la Luna y del observador para esta época T0. Calculemos las variaciones horarias de u y v:
(40.10)
Llamando T al instante del contacto y despreciando la variación de L durante el pequeño intervalo τ = T –T0, la ecuación (39.10) queda
Consideremos en la base x,y con origen en el punto en que se proyecta el observador los siguientes vectores (Fig. 12.10)
FIG. 12.10
De la figura 12.10 se deduce:
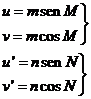(42.10)
y también
(43.10)
siendo
ψ el ángulo que forman 
y 
.
De acuerdo con las relaciones que acabamos de exponer, las ecuaciones (41.10) se pueden escribir en forma vectorial
Multiplicando (44.10) vectorialmente
por 
, obtendremos:
Tomando módulos:
(45.10)
y dividiendo por n:
siendo
Δ la distancia mínima del origen al vector 
.
De (46.10) se deduce que
(47.10)
Si multiplicamos escalarmente (44.10)
por , obtendremos:
de donde:
Si
uu + vv = D
queda
(48.10)
El ángulo ψ dado por (47.10) no queda determinado, obteniéndose por tanto dos valores de ψ que sustituidos en (48.10) nos darán los valores de τ correspondientes al principio (τp) y fin (τf) del eclipse. Se toma
para el principio 
para el final 
Puesto que L no se conoce, para calcular (47.10) y (48.10) partiremos de un valor aproximado que nos proporcionará unas épocas aproximadas. Obtenidas éstas, corrientemente debe aplicarse de nuevo el método (una o más veces) tomando dichas épocas como de partida en cada caso y efectuando les cálculos por separado.
b) Máxima fase del eclipse: Podemos calcular también
el instante de la máxirna fase del eclipse, la cual tendrá lugar cuando
la distancia aparente Luna-Sol sea mínima, condición que es equivalente a decir
que L - es máxima y despreciando
la variación de L es lo mismo que
decir que es mínima.
De (44.10) suponiendo que partimos
del valor = L, tenemos:
(49.10)
y
observando la figura 13.10 vemos que 
será mínimo
cuando alcance el valor Δ, con lo cual y serán perpendiculares,
es decir:
o también.
FIG. 13.10
de donde:
(50.10)
Dicho
valor (50.10) de τ nos dará, sumado a T0, la época de la máxima
fase del eclipse.
c)
Ángulo de posición de los puntos de contacto:
El ángulo de posición del punto en que la Luna encuentra el borde del Sol al comienzo del eclipse será (Fig. 12.10):
(51.10)
siendo
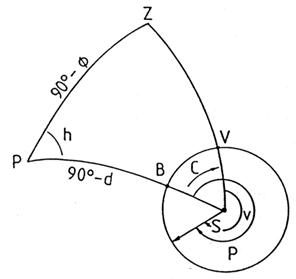
El ángulo de posición P lo tomaremos a partir del punto boreal B del Sol (punto más cercano al polo norte) hacia el este. Llamaremos vértice V del limbo al punto más alto del disco. Al ángulo de posición del punto de contacto respecto del
FIG. 14.10
vértice del limbo le designaremos por V (Fig. 14.10). Si C es el ángulo paraláctico en el Sol, podernos escribir
Aplicando la segunda y tercera fórmulas de Bessel al triángulo PSZ, tendremos:
(53.10)
Suponiendo en las fórmulas (23.10) ρ = 1, 
, las coordenadas del observador nos quedarán
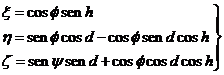(54.10)
que sustituidas en (53.10) nos darán:
(55.10)
de donde
(56.10)
con C tal que sen C tenga el mismo signo que ξ.
El ángulo paraláctico así deducido para el principio y el fin del eclipse, combinado con el correspondiente valor de P, nos suministra mediante (52.10) los respectivos ángulos de posición V de los contactos.
d) Grado de oscurecimiento: Llamaremos grado de oscurecimiento G en una época
T a la fracción de diámetro aparente del Sol que está cubierta por el
disco lunar. Con mucha aproximación se tendrá (Fig.15.l0)
(57.10)
siendo
L1 y L2 los radios de la penumbra y de la sombra
respectivamente y la distancia del
observador al eje de sombra (recordemos que L2
es negativo).
e) Magnitud del eclipse: En particular, llamaremos magnitud del eclipse al grado de oscurecimiento
FIG. 15.10
máximo,
el cual tendrá lugar, evidentemente, en el instante de la máxima fase ( mínima):
(58.10)
Recordando las fórmulas (34.10) y (32.10) y teniendo en cuenta que f1
f2, podemos escribir:
L1 + L2
l1 + l2 2 z tan f2(l1 - k) 2(L1 – k)
y
(59.10)
fórmula aproximada que sólo se aplica para los eclipses parciales.
En los Anuarios, junto a los elementos referentes a los eclipses de Sol que ocurren en el año, se incluyen mapas de los que pueden deducirse valores aproximados de las circunstancias para un lugar determinado. Veamos de una forma elemental cómo se construyen tales mapas.
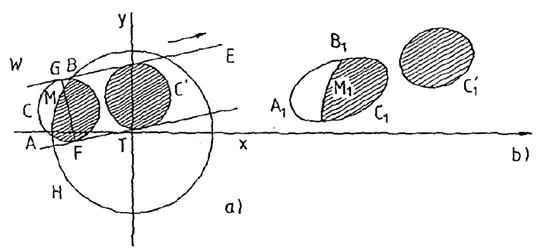
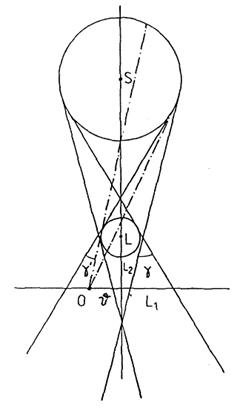
Representemos la sombra proyectada sobre el plano
fundamental, suponiendo la Tierra esférica y despreciando la refracción (Fig. 16.10). Sean H
la intersección de la Tierra con el plano fundamental; C la intersección del cono de penumbra con dicho plano. Supongamos
que reemplazamos el cono de penumbra por un cilindro de revolución que tiene el
mismo círculo de base C en el plano fundamental. La proyección ortogonal sobre
el plano fundamental de la curva intersección del cilindro de base C con la superficie de la Tierra es la
circunferencia C (Fig.
16.10, a) cuya
proyección cartográfica es
una curva C1
(Fig.
16.10, b). Distinguiremos dos casos según que C y H sean secantes o C sea interior a H (C en la Fig.a)).
FIG 16.10
Si C y H son secantes, en un instante dado, la región desde la cual el eclipse es visible como eclipse parcial está limitada por una parte de la transformada C1 de C y la transformada A1B1 del arco AB de H.
Si C es interior
a H la región desde la cual el
eclipse es visible está limitada por la curva 
.
El conjunto de puntos de la Tierra desde los que se puede observar el eclipse parcial se obtiene determinando la envolvente de las curvas C1. Para la determinación de esta envolvente se ha de tener en cuenta el desplazamiento de la sombra en el plano fundamental (de oeste a este) y la rotación de la Tierra. La transformada de C es móvil y permanece constantemente tangente a dos paralelos terrestres.
El eclipse general comienza y termina en los instantes en que los círculos C y H son tangentes exteriores (recordar 37.10).
Supongamos C y H secantes y que los puntos de intersección A y B corresponden a la salida del Sol. Para un observador situado en A el eclipse termina en este instante; en efecto, la sombra deja este punto para dirigirse al este. En cambio, para un observador situado en B el eclipse empieza al orto ya que la sombra comienza a cubrirle.
Admitamos que el radio de C sea invariable y que su círculo se desplaza en el plano fundamental con movimiento rectilíneo y uniforme. En estas condiciones, C permanece tangente a dos rectas paralelas pasando por F y G. Un observador que estuviera quieto con relación a los ejes de coordenadas observaría el medio del eclipse y el máximo de su magnitud cuando el diámetro FG pasase por el lugar que ocupa dicho observador. Así pues, un observador situado en M vería el medio del eclipse al salir el Sol.
Teniendo en cuenta el desplazamiento de la sombra en el plano fundamental y la rotación de la Tierra se pueden determinar
sobre el mapa los
lugares de los puntos A, B y M.
Son las curvas siguientes (Fig. 17.10):
1.- Principio del eclipse al orto
2.- Máximo del eclipse al orto
3.- Fin del eclipse al orto
4.- Fin del eclipse al ocaso
5.- Máximo del eclipse al ocaso
6.- Principio del eclipse al ocaso
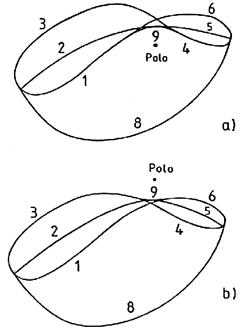
Para acabar con la determinación del dominio de visibilidad, hemos de trazar sus límites boreal y austral. Cuando en la mitad del eclipse general el círculo C es interior al H (Fig. 16.10), la envolvente de las curvas C1 se compone de dos curvas (7 y 8 de la
FIG. 17.10
Fig. 17.10) que difieren poco del lugar de los puntos F y G respectivamente. Si los círculos C y H son siempre secantes hay una sola de estas curvas (7 u 8) y los arcos 1, 3, 4 y 6 forman una sola curva con un punto doble, la cual con el límite boreal o austral delimita el dominio de visibilidad (Fig. 18.10). Hace falta añadir entonces el arco 9 de paralelo terrestre al cual la proyección cartográfica de H permanece tangente. Según que el polo P pertenezca o no al dominio de visibilidad el arco 9 se dispondrá según indica la Fig. 18.10. Entre este arco y los 3 y 6 hay una pequeña región en la cual el Sol se pone y sale eclipsado, es decir que el medio del eclipse tiene lugar por la noche.
FIG. 18.10