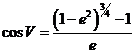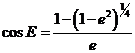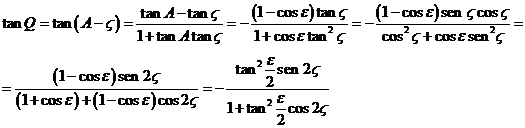4.7 Ecuación del centro y reducción al ecuador
Como ya indicamos en el apartado
1.7, al describir el Sol su órbita aparente de acuerdo con la ley de las
áreas, no es uniforme la variación de su longitud. Aunque lo fuese, no lo sería
la variación de su ascensión recta. Para poder utilizar las observaciones del
Sol para la medida del tiempo y así llegar a definir el Sol medio, se impone
estudiar con detalle tales hechos.
Según vimos al principio de este capítulo, y
continuando con la misma notación, en la órbita aparente del Sol se verifica
(fórmulas (1.4) y (2.4)):
Llamamos ecuación
del centro a la diferencia entre
las longitudes verdadera y media del Sol:
y es, por tanto, la corrección que hay que aplicar a la longitud L de un sol ficticio para obtener la longitud V del sol
verdadero.
Recordando la fórmula que suministra la anomalía
verdadera en función de la media (apartado 3.6) :
![]()
la ecuación del centro puede expresarse, según (32.4),
en función de la longitud media L del
Sol:
![]() (34.4)
(34.4)
Ceros de la ecuación del centro: Según (33.4) la ecuación del centro se anula en los extremos de la línea de los ápsides (perigeo y apogeo), puesto que en este caso M y V toman el mismo valor ( 0º y 180° respectivamente).
Máximos
y mínimos de la ecuación del centro: De las fórmulas del movimiento elíptico se desprende inmediatamente que
la ecuación del centro se mantendrá positiva entre el perigeo y el apogeo en la
primera mitad de la elipse y negativa entre el apogeo y el perigeo en su
segunda mitad. Pasará, por tanto, por un máximo en la primera mitad de la
elipse y por un mínimo en la segunda, siendo simétricos respecto a la línea de
los ápsides. Dichos valores extremos los podremos obtener suponiendo la
anulación de la primera derivada de la ecuación del centro, teniendo en cuenta
que ![]() y la expresión de la
ley, de las áreas
y la expresión de la
ley, de las áreas ![]() , es decir:
, es decir:
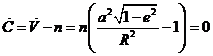
Luego, en el máximo de la ecuación del centro:
O sea que el radio vector es media geométrica
entre los semiejes mayor y menor. Comparando (35.4) con
la ecuación polar de la elipse:
![]()
Y eliminando R
entre ambas, tras sencillas operaciones se obtiene:
Análogamente, eliminando R entre (35.4) y la relación
R = a (1- e cos E)
fácilmente se obtiene:
Siendo, según (36.4) y (37.4) V > p/2 y E
< p/2, la ecuación del centro pasa por su máximo
en un punto de la órbita comprendido entre los extremos del parámetro y del eje
menor. Dicho máximo puede calcularse, conocidas las correspondientes V y E
por (36.4) y (37.4), buscando M por la ecuación de Kepler
y efectuando la diferencia V- M.
Para el Sol, e = 0,0168, la aplicación de las
fórmulas anteriores suministra los valores:
V = 90º 43' 30" ; E = 89º 45' 20" ; M = 88º 47' 35" ; C = 1º 55' 55"
Llamamos reducción
al ecuador a la corrección que hay que aplicar a la longitud V del Sol verdadero para obtener su ascensión recta A, es decir:
Dividiendo la segunda por la primera de (5.4), poniendo V en lugar de I,
obtenemos la fórmula
![]()
con lo que, procediendo de manera análoga a
como lo hicimos en 2.6,
Y, dado que Q
es siempre un ángulo muy pequeño, sustituyendo tanQ por Q y desarrollando el denominador en serie:
![]()
resulta:
![]() (40.4)
(40.4)
desarrollo en serie que converge rápidamente puesto que ![]()
Ceros
de la reducción al ecuador: Según (39.4) la reducción al ecuador se anula para tanV = 0
y tanV = ¥, es decir, cuatro veces en el transcurso de un
año, para V = 0°, V = 90°, V = 180°, V = 270°, lo cual tiene lugar en los equinoccios y
en los solsticios. Como Q es una
función continua, ello implica la existencia de cuatro extremos (máximos o
mínimos).
Máximos
y mínimos de la reducción al ecuador: Para hallar los máximos y mínimos de Q
con respecto a V, bastará hallar los de tanQ con respecto a tanV al ser la tangente una función monótona
creciente. Derivemos, pues, respecto a tanV la ecuación (39.4) e igualemos a cero. Tendremos:
![]()
y, por tanto, Q pasa por un máximo
para:
Según (39.4), para dicho
máximo es
Haciendo e=23° 27' en (41.4) y (42.4) se obtiene:
V = ± 46° 14' ± 180º
Q = ± 2° 28'