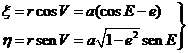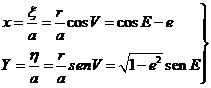3.6 Movimiento elíptico.

El estudio del movimiento elíptico de un astro se simplifica notablemente introduciendo los ángulos o anomalías que definimos a continuación:

Anomalía verdadera : Es el ángulo formado por el radio vector del astro Q y la dirección del periastro P (la teníamos ya definida).

Anomalía excéntrica: Es el ángulo formado por la dirección del periastro y el radio CQ', siendo C el centro de la elipse y Q' la intersección con el circulo principal de la elipse, de la normal por el astro Q al eje mayor de la elipse.

Anomalía media: Es el ángulo M descrito con vértice en el foco O, en sentido antihorario y a partir de la dirección del periastro, por un astro ficticio que gira con velocidad angular igual al movimiento medio n=2p/P (P=periodo del movimiento). Si empezamos a contar el tiempo en el instante de paso del astro por el periastro, la anomalía media valdrá nt. En general será:

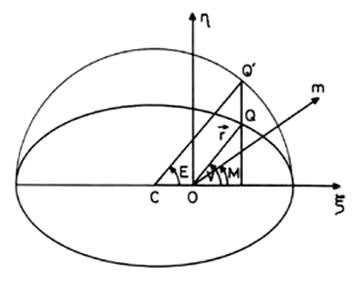
FIG 6.3

(35.3)

donde T es la época de paso por el periastro.

Es cómodo expresar las coordenadas polares de un astro en función de la anomalía excéntrica; para ello, tomemos un sistema de ejes cartesianos x ,h con origen en el foco O, y sean (x, h) las coordenadas del secundario Q en dicho sistema. Se verifica:

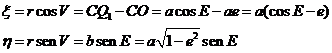
(Obteniendo esta segunda ecuación teniendo en cuenta la razón de afinidad de la elipse y la circunferencia).

En resumen, pues:

(36.3)

y tomando como unidad a, en el mismo sistema de ejes

(37.3)

que son las llamadas coordenadas reducidas del secundario.

De las relaciones (36.3) elevando al cuadrado y sumando ordenadamente, tenemos:

y siendo a>0, e<l, , extrayendo la raíz cuadrada:

(38.3)

fórmula que suministra el radio vector en función de la anomalía excéntrica. Si queremos relacionar las anomalías verdadera y excéntrica consideremos la primera de las fórmulas (36.3) y la (38.3):

restando miembro a miembro:

o sea:

(39.3)

y sumando miembro a miembro:

o sea:

(40.3)

Dividiendo ordenadamente (39.3) y (40.3) y extrayendo la raíz cuadrada:

(41.3)

fórmula que suministra la anomalía verdadera en función de la anomalía excéntrica.

3.6.1 Ecuación de Kepler

Relacionemos, finalmente, las anomalías media y excéntrica. Partiendo de la ley de las áreas en su forma polar

(42.3)

y recordando que , se tiene:

e integrando entre O y V, valores que corresponden respectivamente a la época T de paso por el periastro ya una época t cualquiera, tenemos:

o sea:

(43.3)

Para efectuar la integración indicada, calculemos dV diferenciando en (41.3):

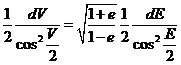
de donde:

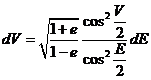
y teniendo en cuenta (40.3), sustituyendo y simplificando:

Sustituyendo en la integral (43.3), recordando que r=a(1-ecosE), resulta:

o sea:

(44.3)

relación buscada que recibe el nombre de ecuación de Kepler.

3.6.2 Métodos de resolución de la ecuación de Kepler

Observemos en primer lugar que si en (44.3) damos a M un valor comprendido entre kp y (k+1)p, con k entero, dicha ecuación admite una única raíz entre tales límites. En efecto, si ponemos

se tiene:

y

Además,

siempre;

luego, la función F(E) es creciente en el intervalo (kp, (k + 1)p) y toma en sus extremos valores de signos contrarios. Luego tiene una única raíz en dicho intervalo.

Entre el gran número de métodos para resolver la ecuación de Kepler citaremos:

a)Método gráfico (o de Dubois). Dibujada una sinusoide, expresando el argumento en radianes, por P tal que OP=M se traza una recta que forme con el eje de abscisas un ángulo a, tal que

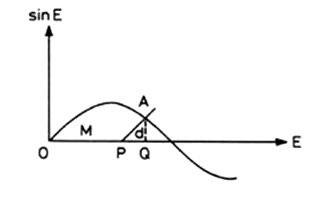
FIG 7.3

La abscisa OQ del punto A de intersección de dicha recta con la sinusoide es OQ=E. En efecto,

Si la escala es grande, en la mayoría de los casos, este método permite obtener E con una aproximación de 1°, sirviendo este valor aproximado como argumento inicial para aplicar otros métodos.

b) Método numérico (o de Newton). Sirve para corregir el valor de la anomalía excéntrica dada por el procedimiento anterior.

Supongamos que por el método gráfico hemos encontrado una anomalía E_O. Sustituyendo en la ecuación de Kepler tenemos:

(45.3)

Si M es el valor exacto de la anomalía media y E el valor exacto de la anomalía excéntrica, tenemos:

DM_o = M -M_o

o lo que es lo mismo:

M = M_o + DM_o

y

(46.3)

Sustituyendo estos valores en la ecuación de Kepler:

y siendo DE_o muy pequeño y teniendo en cuenta (45.3)

O sea:

donde e está expresado en radianes. Conocido DE_o con (46.3) tendremos el valor de E. Llamémosle E₁. Podemos hallar el correspondiente valor de M₁. Si en el orden de aproximación requerida M₁=M daremos por terminado el proceso; si no, seguiremos.

Existen tablas que suministran directamente E en función de e y de M. Este valor de E es aproximado y se corrige con el proceso que acabamos de exponer.

c) Método de Kepler. De la ecuación de Kepler, tenemos:

con e y M dados. Tomando en el segundo miembro como E aproximada el valor de M, resulta:

Tomando ahora, como E aproximada el valor E₁ obtenido:

Repitiendo el proceso iterativamente, podemos obtener la anomalía excéntrica con la precisión deseada.

En general:

d) Método del desarrollo en serie. Consiste en expresar E por desarrollo en serie de Mac-Laurin de potencias de e, considerando M como parámetro. Lo estudiaremos en el apartado siguiente formando parte de un contexto más general.

ANTERIOR

ÍNDICE

SIGUIENTE