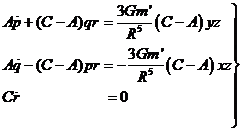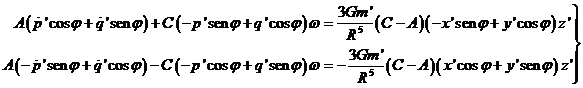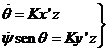2.6 Rotación forzada
Hemos
visto en el apartado anterior que tomando como origen el centro de gravedad de
la Tierra, podemos considerar dos sistemas de referencia: uno de ejes móviles
con la Tierra x,y,z, y otro X,Y,Z, fijo en el espacio. Según el
teorema del momento cinético, designando, como antes, por 
el momento
cinético de las fuerzas exteriores en el sistema móvil, se tiene ahora
(51.2)
donde supondremos que no es nulo y que, en
particular, es debido a la interacción gravitatoria con un astro, que consideraremos
puntual, de masa m' y radio vector 
.
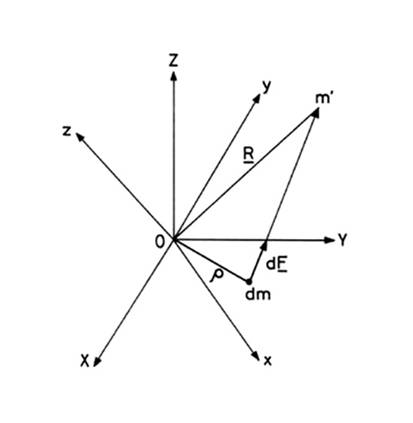
FIG 15.2
Sobre
cada elemento de masa dm de la Tierra
de vector de posición 
y distancia p al astro, actúa una
fuerza
Así
pues, sobre la Tierra actúa un sistema de fuerzas que sabemos que siempre puede
reducirse a una resultante general y a un momento resultante. La resultante
será:
(V potencial terrestre)
y el momento resultante
es decir
(52.2)
Sustituyendo
en (52.2) la expresión (34.2)
que obtuvimos para el gradiente del potencial terrestre
y teniendo en cuenta que 
, obtenemos para el
momento de las fuerzas exteriores en el sistema móvil:
Sustituyendo
en (51.2)
pero
; y, si suponemos la Tierra rígida, I es constante, por lo que 
, es decir:
ecuación diferencial que
recibe el nombre de ecuación de Euler
generalizada. Para resolverla procederemos análogamente al apartado
anterior. Consideraremos que los ejes x,y,z son los ejes principales de inercia
de la Tierra y que la distribución de masas de ésta presenta simetría de
revolución alrededor del eje z. Con esto reducimos el tensor I a su forma
diagonal con los dos primeros elementos de la diagonal principal iguales
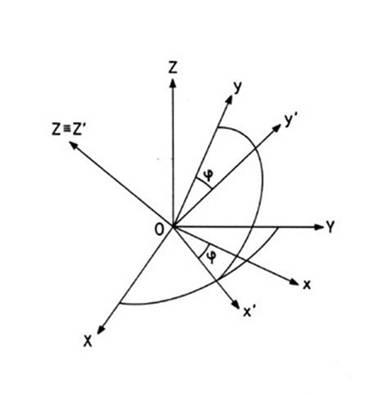
FIG 16.2
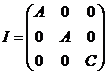
Si
las componentes de en x,y,z son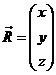 
y las de 
son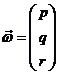 
, la ecuación generalizada de Euler adopta la forma:
(53.2)
Como
en la rotación libre, también ahora es constante la componente r de la
velocidad de rotación .
Realicemos
ahora un cambio de la base x,y,z a la
base x',y',z' definida de la
siguiente forma:
x' determinado por la intersección de los planos XY y xy;
z'=z; y' ortogonal a los anteriores
en sentido directo. Para ello efectuaremos un giro de ángulo ‑j
alrededor del eje z=z'
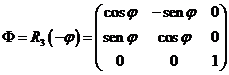
de manera que si
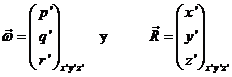
se verifica, por ejemplo,
que
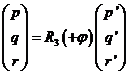
es decir:
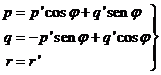
y derivando:
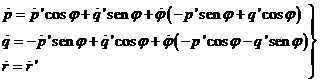
o sea:
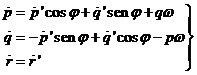
dado que como ya se ha
visto en el apartado anterior, el eje instantáneo de rotación es muy próximo al
eje z y, por lo tanto, 
resultando 
Sustituyendo
en las dos primeras ecuaciones de (53.2) las expresiones
anteriores, resulta:
sistema que es equivalente
a:
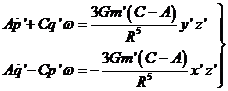(55.2)
que resulta de multiplicar
primero la primera ecuación de (54.2) por cosj y
la segunda por senj y
restar de la primera la segunda y después multiplicar la primera por sen j y
la segunda por cos j y
sumar.
Experimentalmente
se demuestra que p y q varían muy lentamente, por lo que
también variarán muy lentamente p' y q', y en una primera aproximación,
podremos considerar nulas sus variaciones 
, 
, obteniendo
(56.2)
que constituye la solución
buscada y donde
con 
, constante que recibe
el nombre de achatamiento dinámico de la
Tierra.
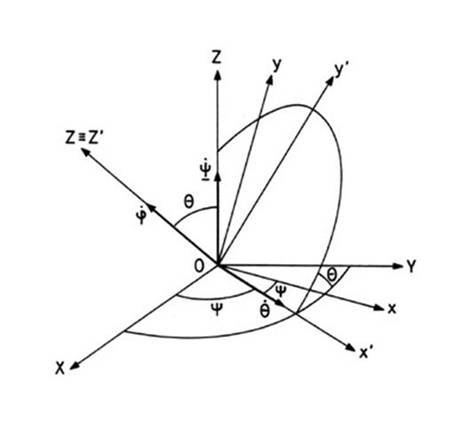
La
posición del triedro móvil x,y,z con
respecto al inercial X,Y,Z suele
darse mediante los ángulos de Euler. De entre las diversas convenciones
existentes la más común en Astronomía es la indicada en la Fig.
17.2, donde:
y =
ángulo de precesión
q =
ángulo de nutación
j =
ángulo de rotación propia
FIG 17.2
Si
el único movimiento fuese el de rotación de la Tierra alrededor del eje z,
variaría sólo j, 
sería su velocidad
angular y y y q
se mantendrían constantes. Pero, supongamos que varían los tres ángulos: w
será la rotación instantánea del triedro x,y,z
(ligado a la Tierra) cuyas componentes en dicho triedro móvil son 
, las cuales expresaremos en función de los ángulos y, q y
j . w
será la suma de las rotaciones debidas a cada ángulo: 
. Proyectaremos sobre los ejes x,y,z y
sumaremos las proyecciones:
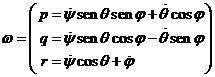(57.2)
como que 
y 
, la última componente queda reducida a
Nos
interesa obtener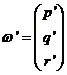 
en la referencia
x',y',z'. Para ello proyectaremos sobre estos ejes y sumaremos. Obtendremos:
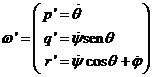
Sustituyendo
estos valores en (56.2) queda finalmente el sistema
(58.2)