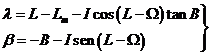9. MOVIMIENTO DE LA LUNA
9.1
Rotación de la Luna. Leyes de Cassini
Es un hecho de observación corriente que la Luna presenta siempre la misma cara hacia la Tierra; dicho de otra forma, vemos los accidentes de su superficie siempre aproximadamente en la misma posición sobre el disco. Interpretamos esta observación como una prueba de la rotación de la Luna alrededor de un eje que forma con el plano de su órbita un ángulo poco distinto de 90º, siendo la duración de la rotación igual a la de su revolución sideral alrededor de la Tierra. Las leyes por la que se rige esta rotación fueron enunciadas por J.D. Cassini en 1721 quien las dedujo de la observación. Posteriormente, Lagrange y Laplace las incorporaron a la Mecánica Celeste, admitiendo que la forma de la Luna es similar a la de un elipsoide de tres ejes cuyo eje mayor está constantemente dirigido hacia la Tierra, coincidiendo el eje menor con el de rotación de la Luna. De todos modos, por diferir muy poco entre sí las longitudes de los ejes de dicho elipsoide, en el estudio de las libraciones, si interesa, se puede considerar la Luna esférica.
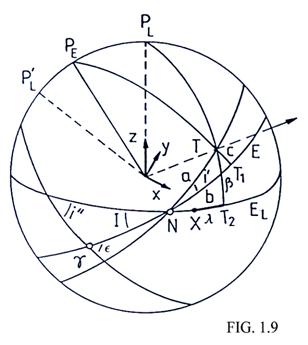
Sea (Fig.l.9) N el nodo descendente del ecuador lunar sobre la eclíptica. Las leyes de Cassini pueden enunciarse de la siguiente forma:
1ª) El nodo N coincide sensiblemente con el nodo ascendente medio de la órbita lunar.
2ª) La inclinación I del
ecuador lunar sobre la eclíptica es sensiblemente constante ( I = 1º 32
6
). La inclinación media del ecuador lunar sobre la órbita es i + I = 6º 41.
3ª) Si X es el punto hacia el
cual va dirigido el eje mayor del elipsoide al que se asimila la Luna, la suma
de los arcos 
y NX es aproximadamente igual a la longitud media de la Luna disminuida
en 180º.
Las leyes de Cassini son aproximadas. La coincidencia de los nodos no es rigurosa, de modo que en N no tenemos un punto sinó un pequeño triángulo; la inclinación I presenta fluctuaciones de amplitud muy pequeña, y la dirección del eje mayor puede separarse algunas centésimas de grado de la que hemos definido. Estas pequeñas desviaciones constituyen la libración física que se determina a partir de la teoría dinámica de la rotación de la Luna.
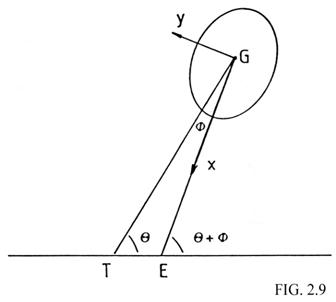
Sea (Fig. 2.9) x, y, z un sistema de coordenadas rectangulares selenocéntricas cuyos ejes coinciden con los ejes principales de inercia de la Luna y su origen con el centro de gravedad de la misma; el eje x orientado hacia la Tierra, el eje y perpendicular a él de modo que el sistema esté orientado en sentido directo y el eje z en la dirección del eje de giro de la Luna. Por otra parte, sean, con respecto a estos ejes, p, q, r los cosenos directores del eje de la eclíptica y l, m, n los del radio vector Tierra-Luna. p, q, m y n son pequeños mientras que r = l » 1.
Supongamos la Tierra esférica, de masa M y a una distancia R, constante, de la Luna y llamemos A, B y C a los momentos de inercia de la Luna con relación a los ejes coordenados. Sean (wx, wy, wz) las componentes de la velocidad angular de la Luna en dicho sistema x, y, z. Las dos primeras son pequeñas y sus cuadrados y productos podrán despreciarse.
Recordemos la ecuación de Euler generalizada relativa al movimiento de un cuerpo en rotación (2.6):
(1.9)
donde I es el tensor de inercia que en el caso que estamos considerando se escribe
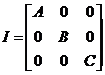(2.9)
y 
el momento de las fuerzas
exteriores que supondremos limitadas a la de atracción de la Tierra,
(3.9)
Desarrollando (1.9) tendremos:
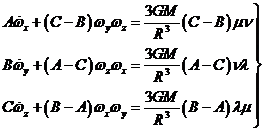(4.9)
y despreciando cantidades pequeñas de segundo orden:
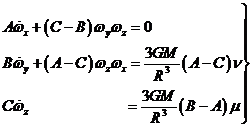(5.9)
Consideremos la tercera ecuación de (5.9) que por
contener solamente 
puede ser estudiada
independientemente de las otras. Supongamos (Fig. 2.9) que
la dirección TG forma un ángulo q con una dirección determinada y llamemos f al ángulo TGE. f nos da la medida de la libración en longitud. La dirección GE forma un ángulo q + f con la dirección
fija. Una rotación positiva alrededor del eje z, wz haría disminuir el ángulo q + f, por
consiguiente:
Ahora bien: 
por tanto, con mucha aproximación, resulta
Supongamos en primer lugar el caso en que la órbita de la Luna es
circular, es decir, 
. La expresión (6.9) describirá un
movimiento armónico simple de la forma:
con
lo cual implica que sea B > A y por consiguiente, si a, b y c son las longitudes interceptadas por la Luna sobre los ejes x, y y z respectivamente, que sea a > b. La solución de (7.9) es
donde a y b son constantes arbitrarias, amplitud y
fase inicial del movimiento armónico que representa (9.9).
Si esta oscilación pudiera ser observada, su periodo nos daría el valor de 
; pero, es demasiado pequeña para ser detectada.
Consideremos ahora la órbita de la Luna no circular. Si la tercera ley de Cassini fuera exacta, sería:
con n constante; por tanto:
(10.9)
Si t se cuenta desde el perigeo, ε es una cantidad pequeña, del mismo orden de f, y q representa la anomalía verdadera. Suponiendo desviaciones periódicas de la ley de Cassini, pongamos:
(11.9)
y derivando dos veces respecto al tiempo, teniendo en cuenta (6.9) y (8.9), tendremos:
o también
En esta ecuación q - nt representa la ecuación del centro de una órbita kepleriana y por tanto se podría expresar por su correspondiente desarrollo en serie; pero, hemos de tener presente que la órbita de la Luna es una órbita perturbada y, por consiguiente, desarrollaremos el paréntesis del segundo miembro de (12.9) en una serie de la forma
que incluirá la ecuación del centro y las desigualdades periódicas del movimiento de la Luna (despreciamos la aceleración secular).
Para resolver (12.9) empecemos por considerar la ecuación
Supongamos una integral particular de la forma
Derivando dos veces
y sustituyendo deducimos el valor de γ
Por otra parte, la solución de la ecuación sin segundo miembro es
Luego, la solución de (13.9) es
y la integral general de la ecuación completa es:
Hemos dicho que la función complementaria (14.9) correspondiente a las oscilaciones libres es demasiado pequeña para ser observada. Los términos de la solución particular corresponden a las oscilaciones forzadas; para que dichas oscilaciones sean observables, en ellos debe ser o H grande o h pequeño.
En la teoría lunar los términos más importantes son el primer término del desarrollo de la ecuación del centro o desigualdad elíptica, para el cual
= 1 mes
anomalístico
y la ecuación anual , para la cual
= 1 año anomalístico
donde g es la anomalía media de la Luna, 
es la anomalía media
del Sol y la unidad de tiempo es el día solar medio.
Sustituyendo los valores (16.9) y (17.9) en los correspondientes términos del segundo miembro
de (15.9), observaremos que, puesto que w es muy pequeño, el segundo de ellos,
esto es, la ecuación anual, proporciona la mayor oscilación forzada. Esta puede
observarse, aunque no con mucha precisión, y puede establecerse el valor de a partir de las
observaciones de su amplitud.
Trataremos ahora las dos primeras ecuaciones de (5.9)
sin tener en cuenta ya la variación en wz .
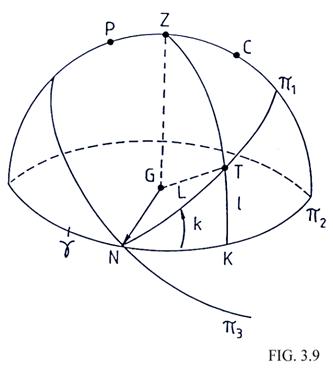
Sea, en la Fig. 3.9, la línea NTΠ1 la órbita de la Tierra alrededor de la Luna en la esfera celeste centrada en la Luna y N su nodo ascendente con respecto a un plano Π2 paralelo a la eclíptica por el centro de la Luna. El círculo máximo que pasa por Z (polo de Π2) y T corta a Π2 en K. El arco KT = 1 es la latitud selenocéntrica de la Tierra. Despreciando la precesión podemos escribir
donde g es la velocidad de retrogradación de los nodos.
Sea k la inclinación de la órbita de la Tierra
con relación a Π2 la
proyección de la retrogradación de N
sobre la órbita de la Tierra durante un tiempo t será un arco 
, pero por ser k muy
pequeño, podemos suponer que dicho arco es gt.
Por tanto, suponiendo que la Tierra se mueve en una órbita circular con
movimiento angular n, podremos
escribir
y
y también
Por consiguiente:
Sean, en la misma figura 3.9, P el polo de Π1 y C el polo de Π3 (plano del ecuador de la Luna). La condición para que P, Z y C estén en un mismo círculo máximo como se requiere en virtud de la tercera ley de Cassini es
donde 
es el vector director
de GC y es el vector director
de la línea de los nodos, ya que, en efecto, si N es el polo del círculo máximo que pasa por P y Z, y C ha de estar en este mismo círculo, los
vectores y han de ser
perpendiculares.
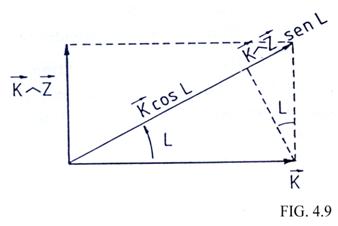
Podemos calcular a partir de 
y 
indicando por y 
los vectores
directores de GK y GZ respectivamente, suponiendo 
(Fig.
4.9)
Ahora bien, si designamos por 
el vector de posición
selenocéntrico de la Tierra, es:
y
recordando la propiedad del triple producto vectorial 
y tomando senZT = 1 es:
Por consiguiente:
es decir, desarrollando:
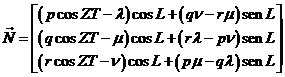
y multiplicando escalarmente por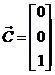 
,
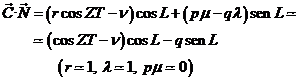
y teniendo en cuenta que cosZT = p+v, también
Sea por otra parte, con respecto a los ejes móviles x, y, z (Fig. 2.9):
puesto que en
virtud de la segunda ley es fijo en el espacio.
Desarrollando (20.9), tendremos:
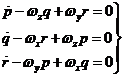(21.9)
o también, dentro de la aproximación en que nos movemos (tomamos wz = n):
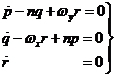(22.9)
Derivando las dos primeras respecto al tiempo y teniendo en cuenta la tercera obtenemos:
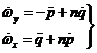(23.9)
y sustituyendo en las dos primeras ecuaciones de (5.9), dividiendo por A la primera y por B la segunda, tomando r = 1 y recordando (18.9) tendremos:
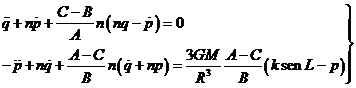(24.9)
Haciendo para simplificar
teniendo además en cuenta
que 
, las ecuaciones (24.9) se escribirán:
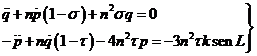(25.9)
La solución de estas ecuaciones constará de una función complementaria, que representará las oscilaciones libres y una integral particular procedente del término en sen L, que dará las oscilaciones forzadas.
Las oscilaciones libres han de ser estables. Hallaremos las condiciones para que así sea:
Supongamos que
son soluciones de las ecuaciones (25.9) sin segundos miembros. La ecuación característica del sistema es:
(26.9)
Para que las oscilaciones sean estables, las dos raíces de esta ecuación, considerada como de segundo grado en s2, deben ser reales y negativas. La condición para que sean reales es
y las condiciones para que sean negativas:
La tercera es equivalente a decir que (C - A)(C - B) > 0 o lo que es lo mismo que si C >B es C >A y si C< B es C<A.
Tanto en un caso como en otro se cumplen las otras dos. Por consiguiente el eje c en la dirección de GZ es a la vez mayor o menor que los otros dos. Es decir, el eje de rotación de la Luna o es el más largo o es el más corto de los ejes de la Luna.
Consideremos ahora las oscilaciones forzadas. Ensayemos una solución de la forma
(27.9)
Sustituyendo en (25.9) con segundos miembros, recordando que
L = nt + gt + c, resulta:
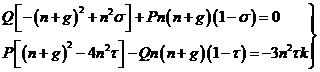(28.9)
ecuaciones que resueltas, eliminando los productos de pequeñas cantidades dan:
(30.9)
y de (29.9)
luego:
(31.9)
lo cual nos dice
que hay una oscilación de pequeña amplitud alrededor de cero. A parte de esta
oscilación, 
es nulo y P, Z y C están en el mismo círculo máximo, propiedad que confirma la
primera ley de Cassini. Se deduce lo mismo si las funciones complementarias se
incluyen en la evaluación de .
Hemos de ver ahora cual es la condición para que Z esté entre P y C; pero, antes, calculemos el valor del
arco 
. Teniendo en cuenta que
elevando al cuadrado
de donde
y por tanto, teniendo en cuenta (28.9) y (29.9) :
(32.9)
Luego, a parte de
una pequeña oscilación, de periodo medio mes nodal, es constante, lo que
prueba la segunda ley de Cassini. Esta pequeña variación en la inclinación del
plano del ecuador lunar sobre la eclíptica da lugar a la llamada libración física en latitud. Los valores
de la libración física oscilan entre -0.º02 y +0.º02.
Supongamos ahora que L = 90º (Fig. 3.9). La Tierra T se hallará en el círculo máximo PZC y tendremos:
Si el eje x corta a la esfera celeste en el punto A, este punto estará muy cerca del círculo máximo PZCE y puesto que CA =90º, para que Z esté entre P y C deberá ser AZ > 90º. Por tanto,
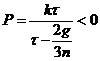(33.9)
y como que 
para que se verifique
(33.9) ha de ser t > 0, lo cual implica que sea C-A > 0 o c < a.
Nos había quedado la duda de si el eje de rotación era el más largo o el más corto de la Luna. De lo que acabamos de decir se desprende que
a> b >c
por consiguiente vemos que c es el menor de los tres ejes.
Aproximando el valor de CZ dado por (32.9) podemos escribir
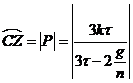(34.9)
de donde
sustituyendo los valores observados = 
, k = 
y g/n=0.00402, hallamos t = 0.00061.
La observación telescópica de la Luna nos dice que los detalles de su superficie no ocupan posiciones rigurosamente invariables sobre el disco, sino que experimentan desplazamientos de cierta amplitud alrededor de una posición media. Damos a dichos desplazamientos el nombre de libración óptica.
Partamos del sistema de coordenadas x, y, z que hemos definido en el apartado anterior al cual referiremos los puntos de la superficie lunar, así como las direcciones selenocéntricas de la Tierra y del Sol. La longitud selenográfica o selenocéntrica se mide sobre el ecuador lunar, en sentido directo, a partir del punto X (Fig. 1.9); la latitud selenográfica o selenocéntrica se mide a partir del ecuador, positivamente hacia el norte. La posición del punto X está definida por la tercera ley de Cassini:
siendo Lm la longitud media de la Luna y W el argumento del nodo.
En la Fig. 1.9, T representa la posición selenocéntrica de la Tierra en la esfera celeste. Sus coordenadas eclípticas son:
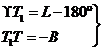(35.9)
donde L y B son las coordenadas eclípticas longitud y latitud de la Luna. Este punto T tiene las mismas coordenadas selenográficas l y b que el punto de la superficie de la Luna que un observador geocéntrico ve en el centro del disco lunar. Es decir
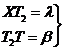(36.9)
l recibe el nombre de libración en longitud y b el de libración en latitud. La composición de estas dos libraciones da lugar a la llamada libración óptica.
Para calcular la libración óptica consideremos el triángulo NTT1 (Fig. 1.9) en el que
(37.9)
Si incrementamos el ángulo J en d J = I y suponemos que el triángulo sigue siendo rectángulo tendremos:
es decir
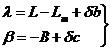(38.9)
Pero, del mismo triángulo NTT1 deducimos:
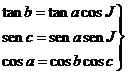
de donde, diferenciando las dos primeras y operando teniendo en cuenta la tercera, resulta:
(39.9)
Sustituyendo en (38.9) y recordando (37.9) obtenemos:
La libración en longitud puede alcanzar un valor de hasta 8º en valor absoluto y la libración en latitud hasta unos 7º.
Para obtener la libración completa sumaremos a estas cantidades las correspondientes a la libración física.
El último término de la expresión que nos da l es de
segundo orden con relación a las inclinaciones I e i; en consecuencia, la libración en longitud difiere poco de las
desigualdades de la longitud de la Luna L
– Lm , cuya parte principal está constituida por la ecuación del
centro de periodo la revolución
anomalística de la Luna como veremos más adelante.
La parte principal de la libración en latitud es 
cuyo periodo es la revolución draconítica. (Cap. 10).
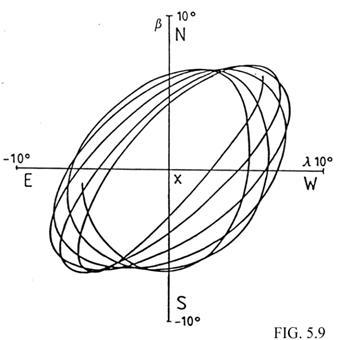
Las dos componentes de la libración óptica tienen periodos distintos lo cual hace que el punto T (Fig. 1.9) describa una curva no cerrada de aspecto parecido al de la Fig. 5.9 que nos permite conocer por una parte el desplazamiento sobre la Luna del punto que, para un observador geocéntrico, se proyecta en el centro del disco y por otra, la órbita selenocéntrica del centro de la Tierra referida al sistema de referencia x, y, z.
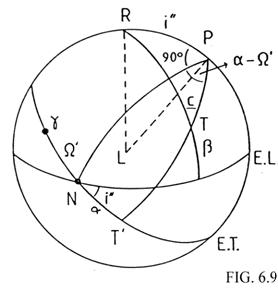
Un dato a tener en cuenta en el cálculo de las libraciones es el valor del ángulo de posición del eje de rotación de la Luna (ángulo C=PTR en la Fig. 6.9)
Aplicando el teorema de los senos al triángulo Polo-Polo de la
Luna-Tierra en el cual es RP = i, RTP = C, RT = 90º - b, RPT= 90º + (a -W) obtenemos:
(41.9)
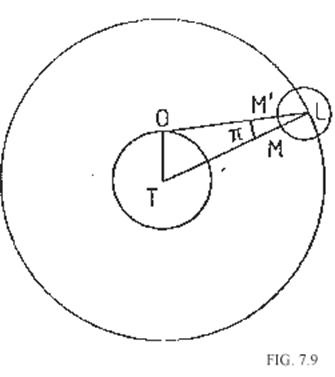
Recibe el nombre de libración diurna el efecto de paralaje debido a que el observador ocupa una posición topocéntrica y, por tanto, el punto que para dicho observador se proyecta en el centro del disco lunar no coincide con el T ( l, b ).
Las rectas que unen el centro de la Luna L con el centro de la Tierra T
y con el observador O forman un ángulo
igual a la paralaje de la Luna ( 
) (Fig. 7.9). Un detalle del disco lunar que
desde T se vería en M desde O se ve en M. Así pues, la libración diurna puede alcanzar el valor de
aproximadamente lº.
La suma de las distintas libraciones alcanza ±9º en longitud y ±8º en latitud, gracias a lo cual podemos ver desde la Tierra 3/5 partes del hemisferio oculto de la Luna.
El cálculo de la libración diurna se reduce al de la paralaje en coordenadas ecuatoriales. Sean Dl y Db la libración diurna en longitud y en latitud y Da y Dd la paralaje diurna de la Luna en ascensión recta y en declinación. Con respecto al punto T de la Fig. 1.9 el punto que representa la dirección selenocéntrica del observador tiene las siguientes coordenadas diferenciales:
(42.9)
Para pasar de un sistema de coordenadas al otro efectuaremos un giro de ángulo C alrededor del tercer eje puesto que éste es el valor del ángulo que forman los planos del ecuador de la Tierra y del de la Luna respectivamente (Fig. 6.9). Tendremos, pues:
(43.9)
(44.9)
La libración total se obtendrá sumando Dl y Db deducidas de (44.9) a l y b respectivamente. El valor topocéntrico del ángulo C se obtendrá sustituyendo los valores topocéntricos de la ascensión recta a y la declinación d de la Luna, en lugar de los geocéntricos, en la fórmula (41.9).