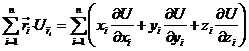7.3 Teorema del virial
Sea J el momento de inercia del sistema definido
por
(22.7)
y derivemos dos veces con respecto al tiempo. Obtenemos:
(23.7)
o bien, teniendo en cuenta (2.7) y (6.7)
(24.7)
Pero,
(25.7)
y si la función f(rik) es del tipo rlik , U es una función homogénea de grado l + 1 (recordar (3.7)
y (4.7)) y en virtud del teorema de Euler el segundo miembro de (25.7) es
(l + l)U,
de donde podemos escribir (24.7) en la forma
y teniendo en cuenta (21.7), también:
(26.7)
En particular, para el caso newtoniano (l = -2) se tiene:
(27.7)
identidad que recibe el nombre de Lagrange-Jacobi.
En (27.7)
T y U son positivos, de modo que si h es positiva, 
es positivo y 
crece indefinidamente,
de modo que por lo menos una de las 
debe crecer hasta el
límite del sistema de los n-cuerpos, lo cual es equivalente a decir que por lo
menos uno de los cuerpos escapa del sistema. Para que el sistema sea estable es
necesario que 
sea negativa y tal que
haga negativo. De todos
modos esta condición no es suficiente para que el sistema sea estable.