3.5 Integral de la
energía.
Multiplicando escalarmente por 
ambos miembros de (9.3) se obtiene:
y como por otra parte,
resulta:
e integrando:
relación que constituye la integral de la energía y que nos indica que el módulo de la
velocidad del secundario sólo depende de su distancia al primario, pues m y h se mantienen constantes durante el movimiento. La constante
escalar h de integración se denomina constante de la energía. Su
interpretación física se halla haciendo tender r a infinito, con lo que v
es v¥ y
Es decir: h
es la mitad del cuadrado de la velocidad en el infinito.
Evidentemente h ha de ser función de las constantes de integración 
y 
. Podemos explicitar dicha dependencia multiplicando
escalarmente por sí misma la ecuación (27.3)
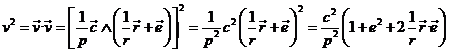
y teniendo en cuenta las igualdades (16.3) y (17.3)
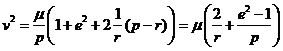
Si identificamos con (29.3)
se deduce:
o en función de c y e :
(30.3)
Ahora bien, 
, y según que la órbita sea elíptica ( e<1), parabólica ( e=1 ) o hiperbólica (e>1), será h<0, h=0 o h>0, respectivamente y, por tanto,
según (29.3) la velocidad en el infinito será imaginaria,
nula o real, respectivamente.
Además, en el caso de la elipse y la hipérbola
el parámetro p es b2/a, por lo tanto:
donde b2
=a2(1 -e2) para la elipse y b2= a2(e2-1) para la hipérbola.
Sustituyendo dichas expresiones en la integral de la energía (29.3)
y operando podemos obtener, en cada caso, el módulo de la velocidad a la
distancia r:
(31.3)
para la elipse, y
(32.3)
para la hipérbola.
En el caso parabólico tendríamos (a = ¥):
La velocidad correspondiente a una órbita
circular de radio r es:
es decir:
que recibe el nombre de velocidad circular.
Si la órbita es parabólica, la velocidad a la
distancia r vale:
(33.3)
valor que recibe el nombre de velocidad de escape a dicha distancia.
Comparando ambas velocidades, observamos que
(34.3)
que nos dice que cuando para una órbita circular
de radio r, la velocidad sea 
, la velocidad tomará el valor de la velocidad de escape y la
trayectoria pasará a ser parabólica.
3.5.1 Velocidades cósmicas. Satélites geoestacionarios.
La mínima velocidad que se debe imprimir a un
cuerpo para que entre en órbita circular alrededor de la Tierra, despreciando
el rozamiento del aire, se denomina velocidad
de satelización o primera
velocidad cósmica. Su valor se halla sustituyendo en la expresión de vc el
radio R y la m de la Tierra:
Llamamos velocidad
de escape o segunda velocidad cósmica
a la mínima velocidad que se debe imprimir
a un cuerpo para que abandone la Tierra. La mínima velocidad se obtendrá si el
cuerpo "llega al infinito" con velocidad nula, por lo que su valor se
podrá hallar sustituyendo la m y
el radio de la Tierra en la expresión de la velocidad parabólica:
Por último se denomina tercera velocidad cósmica a la mínima velocidad que se debe
imprimir a un cuerpo para que, partiendo de la Tierra, abandone el Sistema
Solar. Dicha velocidad se calcula igual que la anterior, pero considerando la m del Sol y tomando como r la distancia de la Tierra al Sol, D:
Si el cuerpo se lanza en la dirección del
movimiento de la Tierra en torno al Sol (unos 29,7km/s, supuesta la órbita de
la Tierra circular), dicha velocidad se reduce a 12,3 km/s.
A menudo interesa, especialmente para
telecomunicaciones, que un satélite artificial se mantenga ubicado sobre la
vertical de un cierto lugar. Ello equivale a decir que la velocidad angular del
satélite (supuesto en órbita circular) sea la misma que la de la Tierra (w).
elevando dicha expresión al cuadrado:
es decir:
Según la tercera ley de Kepler:
por lo que
donde w es
la duración de un día sidéreo en tiempo solar medio (86.164 segundos de t.s.m.). Si h es
la altura del satélite sobre la superficie de la Tierra y R es el radio de la Tierra es
Los satélites situados a dicha altura se
denominan sincrónicos o geoestacionarios.