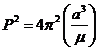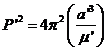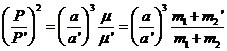3.4 Ecuación de la órbita relativa. Primera y tercera leyes.
De la integral de las áreas (12.3), multiplicando ambos miembros escalarmente por 
, deducimos:
que nos dice que el vector se mantiene
perpendicular al vector constante 
y se mueve en el
plano ortogonal a por el primario;
luego, deducimos que "el secundario describe una órbita plana alrededor
del primario." Veamos cuál es la ecuación de dicha órbita, pero antes hallemos
otra integral primera y, por consiguiente, otra constante de integración.
Calculemos
teniendo en cuenta (9.3) y (12.3) y
utilizando además las relaciones
Tendremos
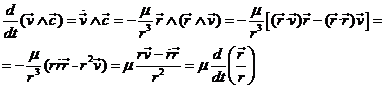
e integrando se obtiene:
siendo (15.3) la integral buscada y
la constante vectorial de integración. Parece, a primera
vista, que 
va a englobar las
tres constantes de integración que nos hacen falta para resolver el problema;
pero, sus componentes no son independientes de las de como luego
veremos. La integral (15.3) recibe el nombre de integral
de Laplace.
Si ahora calculamos c2 teniendo en cuenta (12.3)
y (15.3), tendremos:
y haciendo
obtenemos finalmente:
que es la ecuación de la órbita relativa del secundario alrededor
del primario. Expresada en componentes y racionalizada, constituye la ecuación
de una cuádrica de revolución alrededor del eje dado por . La intersección de dicha cuádrica con el plano en el
que se mueve el secundario, perpendicular al vector constante nos dará la
trayectoria que describe el secundario, que será, en consecuencia, una cónica.
Efectivamente, se encuentra en el
plano orbital, ya que al multiplicar escalarmente los dos miembros de la
integral de Laplace por resulta
Para expresar la ecuación (17.3)
escalarmente, tomemos coordenadas polares de eje polar , polo en el primario y argumento el ángulo V, que llamaremos anomalía verdadera, que forman los vectores y .
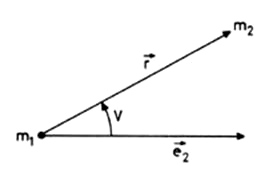
FIG 4.3
Tendremos:
y despejando r :
que es la ecuación polar focal de una cónica de parámetro p y excentricidad
e. El primario ocupa uno de los focos
de la cónica y el vector tiene la dirección
del radio vector del vértice principal más próximo al primario, punto que
recibe el nombre de periastro.
Podemos pues enunciar la primera ley de
Kepler: "en su movimiento relativo el secundario describe una cónica
en uno de cuyos focos se encuentra el primario".
La naturaleza de la cónica (19.3)
depende del valor de su excentricidad e:
Si e<l, es una elipse; si e=1, es una parábola; si e>l, es una hipérbola.
Para los casos de elipse e hipérbola, si
llamamos a y b a los semiejes, el valor del parámetro es p=b2/a. En efecto, si V=0º es, para la elipse:
y para la hipérbola:
y análogamente, si V=180° es,
para la elipse:
y para la hipérbola, como veremos en el estudio del movimiento
hiperbólico, no tiene sentido considerar V=180°.
También podemos escribir el parámetro p en la forma:
en el caso de
la elipse
y
en el caso de
la hipérbola
Si la cónica es una elipse, el semieje a recibe el nombre de distancia media, pues, en efecto, es la
media aritmética de las distancias máxima y mínima al secundario.
Por la segunda ley de Kepler, el movimiento
elíptico será periódico, de periodo P,
con un movimiento medio
(20.3)
Tomando módulos en (13.3):
y según (16.3):
3.4.1 Forma de Newton de la tercera ley de Kepler
Hagamos
aplicación de la fórmula (21.3) para calcular los
periodos de revolución de dos masas m2
y m'2 que describen
órbitas elípticas de semiejes a y a' alrededor de un primario común m1. Llamando P y P'
a los periodos respectivos, tendremos:
Donde
y
con
Dividiendo miembro a miembro (22.3) y (23.3), obtenemos:
que nos dice que "para todas las elipses cuyo valor de m sea el
mismo (m'2 = m2), los cuadrados de los periodos son
proporcionales a los cubos de los semiejes". La tercera ley de Kepler sin tener en cuenta el valor de m se escribiría
La única diferencia entre las ecuaciones (24.3) y (25.3) es el factor
Dividiendo en él numerador y denominador por m1 obtenemos:
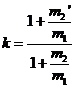
Suponiendo, por ejemplo, que el primario es
el Sol y los cuerpos m2 y m'2 son Mercurio y Júpiter,
respectivamente, tendremos:
y 
resultando ser k
1.
La tercera ley de Kepler (25.3)
es sólo una aproximación de la verdadera ley que relaciona los periodos con los
semiejes (24.3).
3.4.2 Constantes de integración.
Consideremos las constantes de integración y , cada una de las cuales equivale a tres constantes
escalares. Como ya hemos indicado, estas constantes no son independientes ya
que y son dos vectores
perpendiculares (ver 18.3). Se tienen, pues, cinco
constantes independientes, que corresponden a las cinco condiciones que en el
espacio determinan una cónica con un foco prefijado. Recordemos que para
resolver completamente el problema necesitamos seis constantes arbitrarias. La
sexta aparecerá cuando expresemos y 
en función del
tiempo; puede tomarse como constante la época
de paso por el periastro, T.
En función de dicha constante T, y contando las áreas a partir del
periastro, de la ley de las áreas (14.3) se
deduce, para t = T:
de donde
y por tanto,
(26.3)
relación que fija la posición del
secundario sobre su órbita.
3.4.3 Hodógrafa del movimiento
Recordemos que recibe el nombre de hodógrafa
el lugar geométrico de los extremos de los vectores velocidad de un móvil,
trazados, en cada instante, desde un punto dado, exterior a la trayectoria,
llamado polo.
Para hallarla en nuestro caso, multipliquemos
vectorialmente (15.3) por . Obtendremos:
y despejando :
y recordando que 
relación que nos dice que podemos descomponer en suma de dos
vectores no ortogonales:
de módulo
constante c/p y dirección normal a .
de módulo
constante ce/p y dirección la del eje menor, a 90º de en
el sentido del movimiento.
Componiendo ambos vectores se obtiene una
circunferencia como hodógrafa del movimiento. Su radio es c/p y su centro C es el
extremo del radio vector cuyo módulo es ce/p,
normal por el foco a . De la figura 5.3 deducimos las
componentes radial y perpendicular de la velocidad en función de la anomalía
verdadera.
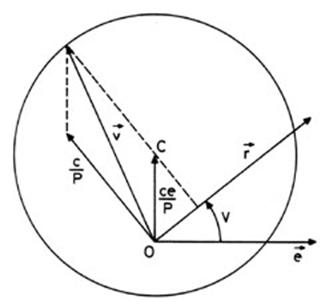
FIG 5.3
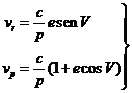(28.3)