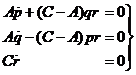2.5 Rotación libre

Consideremos la Tierra como un sólido rígido e introduzcamos dos sistemas de referencia directos: uno inercial X,Y,Z y otro solidario a la Tierra x,y,z ambos con origen en el centro de gravedad de la misma. Interesa estudiar, en los dos sistemas, la rotación de la Tierra libre de fuerzas exteriores.

Sean:

el momento cinético de la Tierra respecto al sistema inercial,

la velocidad angular de la Tierra respecto al sistema inercial,

el momento cinético de la Tierra respecto al sistema móvil,

la velocidad angular de la Tierra respecto al sistema móvil,

I el tensor de inercia de la Tierra,

el momento de las fuerzas exteriores.

En la rotación libre de un cuerpo se considera que, sobre el mismo, no actúan fuerzas exteriores al sistema, por lo que

2.5.1 Movimiento respecto al sistema inercial

En el sistema inercial se verifica

derivando esta expresión respecto al tiempo, teniendo en cuenta que al considerar la Tierra como un sólido rígido es I = cte., tenemos:

(47.2)

pero en un sistema inercial (y sólo en un sistema inercial)

por tanto, en la rotación libre, . Es decir, el momento cinético se mantiene constante con respecto al tiempo. Además, según la expresión (47.2)

(48.2)

que constituye un sistema homogéneo de tres ecuaciones con tres incógnitas (las componentes de ), cuya matriz de los coeficientes es I. Como que el determinante de I no es nulo, la única solución del sistema (48.2) es la trivial:

por lo que también es constante. En conclusión, la velocidad angular de la Tierra se mantiene constante y su eje de rotación permanece fijo en el espacio.

2.5.2 Movimiento respecto al sistema no inercial

Sabemos que la relación entre las variaciones respecto al tiempo de un vector genérico en los ejes inerciales y en los ejes móviles es:

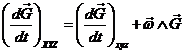
por lo que en particular se verificará:

Pero,

y por tanto:

que es la ecuación diferencial de la rotación libre llamada ecuación de Euler.

Sabemos que si suponemos coincidentes los ejes x,y,z con los ejes principales de inercia de la Tierra y, además, suponemos que la distribución de masas presenta simetría de revolución alrededor del eje z (hipótesis muy próxima a la realidad), el tensor de inercia adopta la forma diagonal

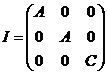
Si designamos por p,q,r las componentes de en el sistema móvil, la ecuación de Euler se escribe:

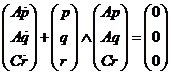
O también:

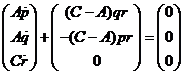
que equivale al sistema de ecuaciones diferenciales de primer orden:

(49.2)

De la última ecuación se deduce directamente que la componente r de según el eje z es invariable.

Si r es constante, también lo será y sustituyendo en (49.2) tendremos

(50.2)

Derivando la primera de las ecuaciones (50.2), obtenemos:

pero, según la segunda

por lo que

cuya solución es

Pero, por el teorema de Euler:

y tomando convenientemente el origen de tiempos:

Sustituyendo en la segunda de las ecuaciones (50.2):

cuya solución es:

En definitiva, la solución del sistema (49.2) es:

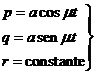
por lo que

es decir, es de módulo constante.

Por otra parte, que la componente r según z de sea constante significa que el extremo de se mueve siempre sobre un plano ortogonal al eje z. Además, el extremo de la proyección sobre el plano x,y de , de coordenadas p,q describe una circunferencia de radio a, parametrizada en z, con una velocidad angular m. Se deduce, por tanto, que describe con velocidad angular m, un cono de revolución alrededor del eje z (tercer eje central de inercia o eje de figura) de semiabertura q constante puesto que como se puede observar en la figura 12.2

FIG 12.2

En suma, el eje instantáneo de rotación describe un cono de revolución alrededor del eje de figura con un periodo

Experimentalmente se ha comprobado que q es del orden de dos décimas de segundo de arco, lo que implica que y, por tanto, que , es decir:

y dado que

(realmente es un día sideral pero la diferencia es despreciable) y del valor teórico

se deduce

P = 305 días sidéreos

Dicho periodo teórico, llamado período euleriano difiere del real observado por Chandler que es de 430 días sidéreos. Newcomb explicó dicha discrepancia suponiendo que la Tierra no era rígida, por lo que los momentos centrífugos no son nulos (I no es diagonal). En el cálculo utilizó los módulos de elasticidad (de Young y de Poisson) obtenidos mediante el estudio de la propagación de las ondas sísmicas. 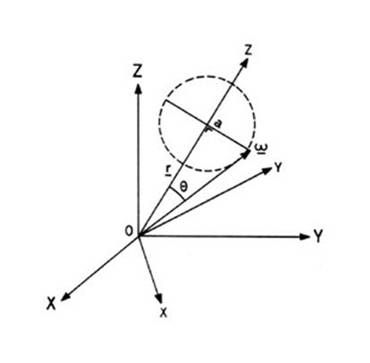Además, existe otro movimiento periódico, de periodo un año y semiamplitud de una décima de segundo de arco, debido a causas meteorológicas. Como que los dos periodos no son conmensurables, ello motiva que, para un observador terrestre, el polo instantáneo P_i se desplace dentro de un cuadrado de lado 0"6 (unos 20 metros), centrado en el polo medio P_m (extremo del tercer eje del elipsoide central de inercia o eje de figura), siguiendo una trayectoria irregular abierta llamada polodia (Fig. 13.2).

FIG 13.2

2.5.3 Variación de la longitud y de la latitud instantáneas de un lugar

Debido al desplazamiento del polo instantáneo variarán las coordenadas instantáneas l,f de todos los puntos de la Tierra.

El eje instantáneo de rotación de la Tierra no se mantiene fijo y, por tanto, el ecuador instantáneo, plano normal a aquél, también variará con el tiempo. Al medir el ángulo formado por la vertical con el ecuador medio y con el ecuador instantáneo, se obtiene, respectivamente, la latitud astronómica media f_m y la latitud astronómica instantánea f.

Interesa conocer las correcciones Df, Dl que deberán aplicarse a las coordenadas medias f_m,l_m, que pueden considerarse constantes, para obtener las instantáneas:

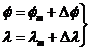
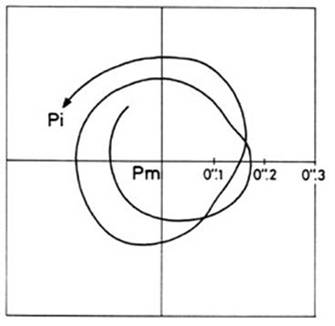
Se trata ahora de expresar Df y Dl en función de la posición del polo instantáneo P_i, sobre la superficie terrestre. Para ello consideraremos dos sistemas de coordenadas cartesianas rectangulares, ambos de orientación inversa, x,y,z y x',y',z', definidos de la siguiente forma: El eje z dirigido hacia el polo medio; los ejes x e y sobre el ecuador medio, de tal modo que el plano zx sea el plano meridiano de Greenwich; el eje z' dirigido hacia el polo instantáneo; el eje x' tomado en la intersección con el ecuador instantáneo del plano determinado por el eje x y el polo instantáneo; el eje y' ortogonal a los anteriores (Fig. 14.2).

FIG 14.2

Las coordenadas esféricas de un punto genérico M situado sobre la superficie terrestre serán (r,f_m,l_m) en el primer sistema y (r',f,l) en el segundo.

Sabemos que el ángulo q formado por el eje z y el z' es muy pequeño, por lo que podemos considerar que el polo instantáneo se encuentra en el plano tangente a la Tierra trazado por el polo medio. Si en dicho plano tangente introducimos unos ejes de coordenadas x,h, paralelos, respectivamente, a los ejes x e y, podremos identificar las coordenadas (x ,h) del polo instantáneo en este nuevo sistema con los ángulos que subtienden desde el centro de la Tierra O.

Para pasar del triedro x,y,z al x',y',z' es preciso realizar una rotación de ángulo ‑h alrededor del eje x (con lo que el eje z pasa a ser z_l y el eje y, y_l), seguida de una rotación de ángulo x alrededor del eje y_l (con lo cual z₁ pasa a coincidir con el eje de rotación instantánea y el eje x x_l pasa a ocupar la posición x'), es decir:

que matricialmente, teniendo en cuenta que la pequeña magnitud de x y h permite sustituir el seno por el arco y el coseno por la unidad, se expresa:

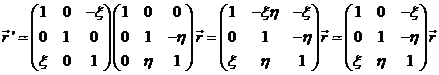
al ser x y h infinitésimos de segundo orden. Además, podemos escribir:

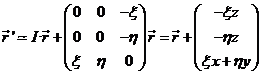
siendo I la matriz unitaria y 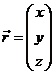por lo que

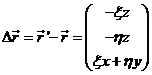
Recordemos ahora las fórmulas de la paralaje diurna en coordenadas horarias (2.2.2)

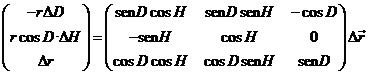
Como que los sistemas de coordenadas que hemos definido son de orientación inversa, al igual que el de coordenadas horarias, podemos aplicar dichas fórmulas directamente haciendo en ellas

con lo que obtenemos:

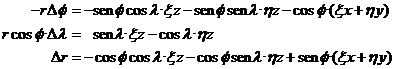
relaciones de las que sólo nos interesan las dos primeras.

Teniendo en cuenta que

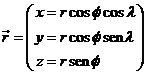
podemos escribir dichas relaciones de la forma:

y, en definitiva:

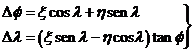
En particular, de la segunda fórmula se deduce que la longitud instantánea de Greenwich no es nula, aunque si muy pequeña, lo que nos autoriza a tomar , , y como , se tendrá:

de lo cual es una cota superior

ANTERIOR

ÍNDICE

SIGUIENTE