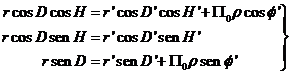2.2 Paralaje diurna

Las distancias a que se encuentran los astros del sistema planetario de la Tierra no pueden considerarse como infinitas respecto a las dimensiones de ésta, y, por ello, las visuales dirigidas a un mismo astro desde lugares distintos de la Tierra no pueden considerarse paralelas. De ahí se deduce la necesidad de reducir todas las observaciones a un mismo punto con objeto de hacerlas comparables. Este punto es el centro de la Tierra. A las coordenadas así obtenidas se las llama geocéntricas, mientras que las relativas a cada observador se denominan topocéntricas. La corrección que hay que aplicar para pasar de coordenadas topocéntricas a geocéntricas recibe el nombre de corrección de paralaje diurna.

2.2.1 Coordenadas horizontales

FIG 6.2

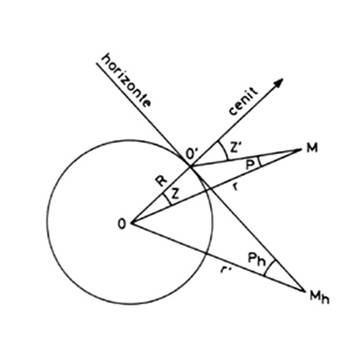
En primera aproximación, para comprender el fenómeno, consideremos la Tierra esférica de radio medio R y estudiemos la corrección de paralaje diurna en coordenadas horizontales. Sea O el centro de la Tierra, O' el observador y M y M_h el astro cuando se encuentra en una posición cualquiera y cuando se encuentra sobre el horizonte de O' respectivamente (Fig. 6.2). El plano de la figura es el plano que pasa por O, O' y M; es decir, el vertical que pasa por M. Dicho plano contiene el cenit del lugar de observación y por consiguiente la paralaje afectará únicamente la altura y no el acimut. Sea r la distancia de M al centro de la Tierra (supuesta constante en el transcurso del día); z la distancia cenital geocéntrica de M y z' la distancia cenital topocéntrica. Sean, además, p la paralaje en altura o ángulo bajo el cual se ve desde M el radio de O' y p_h la paralaje horizontal o ángulo bajo el cual se ve desde M_h el mismo radio. En el triángulo OO'M se verifica:

(15.2)

y en el OO'M_h

(16.2)

o aproximando por el ángulo:

Aplicando el teorema de los senos al triángulo OO'M, tenemos:

es decir,

y por (16.2):

(17.2)

Si exceptuamos los satélites artificiales y la Luna, dada la pequeñez de p y p_h, en (17.2) podemos sustituir los senos por los arcos:

y por (15.2):

(18.2)

igualdades que constituyen la corrección de paralaje diurna en coordenadas horizontales.

2.2.2 Coordenadas horarias

Consideremos ahora la Tierra como un elipsoide de revolución y estudiemos la corrección de paralaje diurna en coordenadas horarias.

Se llama paralaje horizontal ecuatorial p₀ de un astro M el ángulo bajo el cual el radio ecuatorial de la Tierra.

Se verifica:

(recordemos que a = 6.378,140 km).

En el caso del Sol, se designa por P₀ su paralaje horizontal ecuatorial cuando se encuentra a una unidad astronómica de distancia (1 u.a. km). Si se toma como unidad de longitud dicha distancia media, P₀ en segundos valdrá:

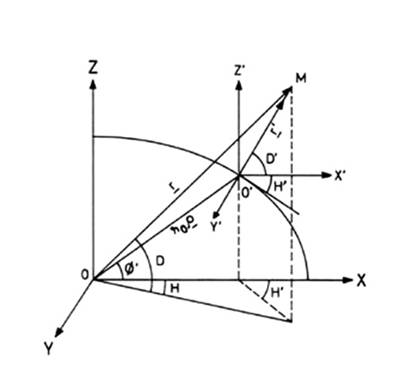
Si medimos P₀ en radianes y las distancias en u.a., el radio del observador será, evidentemente P₀r. Para la deducción de la corrección representamos la traza del elipsoide terrestre por el plano meridiano que pasa por el observador O', y trasladamos su sistema local de coordenadas horarias X’,Y’,Z’, al centro de la Tierra, conservando fijo el plano X’Y’. Tendremos el sistema X,Y,Z, donde XZ define el mismo plano que X'Z' (Fig. 7.2). Sean (r,H,D) las coordenadas horarias geocéntricas de un astro M y (r’,H’,D') las coordenadas horarias topocéntricas del mismo. f' y r se obtienen de f, l, h, supuestas conocidas.

FIG 7.2

Es evidente que

(19.2)

donde r está contenido en el plano meridiano de O'. Expresando (19.2) por sus componentes obtenemos las relaciones

(20.2)

que constituye un sistema de tres ecuaciones que nos permite determinar las tres incógnitas r, H, D. Si el astro M se encuentra muy alejado (), pueden simplificarse los cálculos mediante el empleo de fórmulas diferenciales.

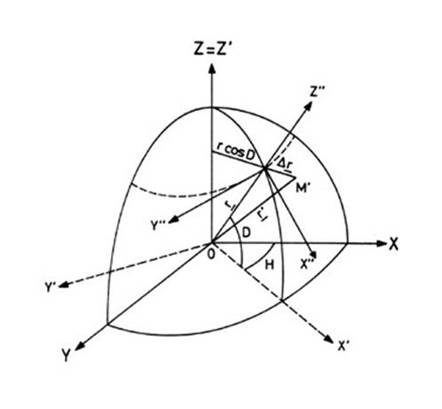
Consideremos el anterior sistema de coordenadas X,Y,Z, de centro O, y un sistema de coordenadas X’’, Y’’, Z’’ (Fig. 8.2) con centro en el astro M definido de la siguiente forma:

FIG 8.2

Eje X" tangente al meridiano de M creciente en el sentido de las declinaciones decrecientes; eje Y" tangente al paralelo de M creciente en el sentido de los horarios crecientes; eje Z" en la dirección y sentido creciente del radio vector , estando los dos triedros orientados en sentido retrógrado. Podemos pasar de una base a otra mediante un número finito de rotaciones.

Si definimos:

(21.2)

siendo las magnitudes con tilde las topocéntricas y las otras las geocéntricas, según (19.2):

y según (20.2):

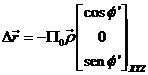
Si consideramos a como un vector libre, lo podemos situar con origen en el astro M y hallar sus coordenadas con respecto a la base X" Y" Z" que obtendremos en función de las correcciones (21.2). Representando las dos expresiones de en esta misma base X" Y" Z" e identificando obtendremos un sistema de ecuaciones cuyas incógnitas serán las correcciones (21.2).

Para ello descompongamos según sus componentes diferenciales en X" Y" Z"

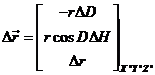
(la primera componente es negativa al considerarla en el sentido de las declinaciones decrecientes). Pasemos las componentes de según XYZ a las componentes según X"Y"Z", para lo cual se precisan dos giros: uno de amplitud H alrededor de Z que transforma X Y Z en X’Y’Z’, y otro de amplitud 90º-D alrededor del eje Y’ que transforma X Y Z en X”Y”Z”.

El primero tiene lugar alrededor del tercer eje, en sentido positivo, luego se consigue aplicando R₃(H); el segundo alrededor del segundo eje y también en sentido positivo, es decir, se consigue aplicando la matriz R₂(90° ‑ D). Luego, tendremos:

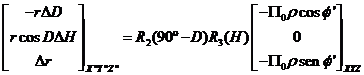
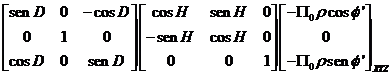
y operando e identificando:

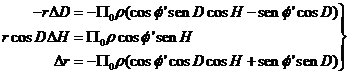(22.2)

En Astronomía de posición sólo se consideran las dos primeras igualdades. Teniendo en cuenta que q=A+H, por lo que, y que viene expresado en segundos de arco, tenemos:

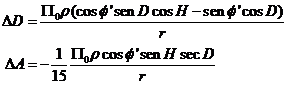(23.2)

donde r se mide en unidades astronómicas y vendrá expresado en segundos de tiempo. Dichas igualdades también se escriben:

donde

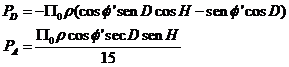
denominándose P_D factor paraláctico en declinación y P_A factor paraláctico en ascensión recta.

Por definición de y es:

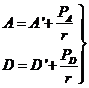(24.2)

Los factores cos y sen se pueden obtener de los Anuarios para distintas latitudes en función de S, C y (ver, por ejemplo, "Efemérides Astronómicas", Instituto y Observatorio de Marina, San Fernando (Cádiz)). Para hallar r se parte observaciones simultáneas de M desde dos puntos distintos de la Tierra. En un mismo instante será:

debiéndose obtener la misma r a partir de las ascensiones rectas y declinaciones. En el cálculo de los factores paralácticos es indiferente tomar coordenadas topocéntricas o geocéntricas.

ANTERIOR

ÍNDICE

SIGUIENTE