3.9 Movimiento parabólico
En el caso de que la trayectoria sea una
parábola es e=1 y por tanto su
ecuación será
![]() (58.3)
(58.3)
o también, teniendo en cuenta que en la parábola es p=2q
siendo q la distancia del foco al
periastro y que ![]() tenemos:
tenemos:
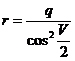 (59.3)
(59.3)
Consideremos ahora un sistema de coordenadas
rectangulares x, h con origen en el foco O (Fig. 9.3).
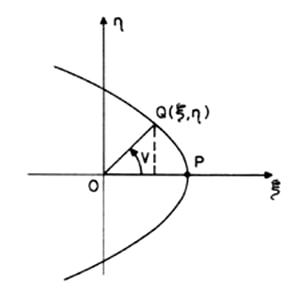
FIG 9.3
Se verificará:
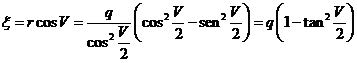
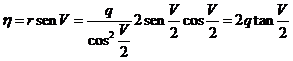
y haciendo
![]()
queda
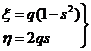 (60.3)
(60.3)
o, también, en polares:
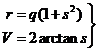 (61.3)
(61.3)
Se trata pues de determinar s, ya que una vez calculada tendremos
inmediatamente las coordenadas cartesianas y polares del astro en su órbita.
Partiendo de la ley de las áreas en su forma
polar y teniendo en cuenta el valor del parámetro p=c2/m , tenemos:
![]()
de donde, teniendo en cuenta la ecuación de la órbita relativa:
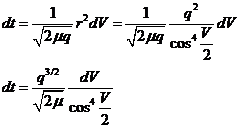
e integrando entre T y t, teniendo en cuenta que para t = T (época de
paso por el periastro) es V =0:
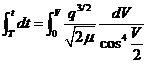
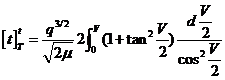
es decir:
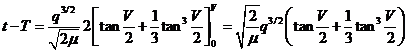
El movimiento parabólico viene pues regido
por la ecuación
que constituye la llamada ecuación
de Barker. Dicha ecuación tiene siempre una única solución. Efectivamente,
si
![]()
como
![]()
f(s) es una función monótona creciente
que pasa por el origen, por lo que presenta un único punto de intersección (que
es la solución) con la recta
![]() (Constante en cada problema).
(Constante en cada problema).
La solución puede hallarse, por ejemplo,
aplicando el algoritmo de Cardano, con lo que resulta:
![]()
donde D es el discriminante
![]()
que es positivo, lo cual indica que la ecuación de Barker tiene una raíz
real y dos complejas conjugadas, como ya hemos demostrado.
La ecuación (62.3) ha
sido también tabulada para diversos valores del primer miembro.
Si en (62.3) se
expresan q y c en unidades astronómicas, se tiene, en días medios,
![]()
Se suele escribir
M(V)= 75s+25s3
y se tabula M(V) (tablas de
Barker). El tiempo transcurrido desde el paso por el perihelio, conocida V, se obtiene de la fórmula
![]()
en la cual el coeficiente de q3/2
resulta de dividir 27d,403895 por 25.
Para q=1,
el tiempo necesario para que la anomalía V
pase de 0° a 90°, variando entonces M(V)
de 0 a 100, es igual a 109d,61 , de donde el nombre de cometa de 109
días dado por los antiguos a un cometa ficticio cuya distancia al perihelio
fuera de 1 u.a.