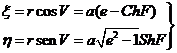3.8 Movimiento
hiperbólico
En el caso de que la trayectoria sea una
hipérbola es e>1 y de la
ecuación
teniendo en cuenta que r debe
ser positivo y p=c2/m, se
deduce que V debe variar entre
de modo que el cuerpo sólo describe una
rama de hipérbola, precisamente la que dirige su concavidad hacia el
foco.
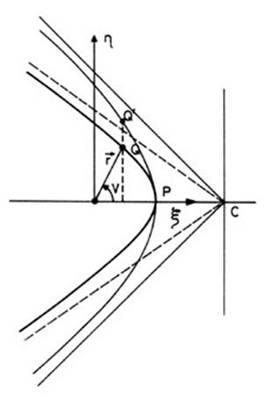
FIG 8.3
Consideremos ahora un sistema de coordenadas
rectangulares x,
h con origen en el foco O. Se verificará:
donde F es el parámetro de la
representación (hiperbólica) de la hipérbola equilátera por
Observamos que las fórmulas (53.3)
se pueden obtener, por analogía con las del movimiento elíptico, sin más que
tomar E=iF, cosFi=ChF, isenFi=-ShF,
y tener en cuenta que a es negativo.
Si elevamos al cuadrado y sumamos los dos
miembros de (53.3), tendremos:
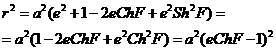
De donde:
Si queremos relacionar la anomalía verdadera
con F, consideremos
restando:
y sumando:
de donde:
(56.3)
Si queremos relacionar F con la anomalía media, escribiremos, de la expresión polar de la
ley de las áreas:
y
y sustituyendo
o también:
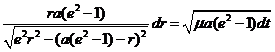
y desarrollando y simplificando:
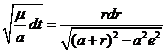
y si hacemos el cambio de variable a+r=aeChF
la integración nos da una ecuación que corresponde a la de Kepler:
(57.3)