1.9 Refracción astronómica
La luz se
propaga en línea recta en el vacío o en los medios transparentes homogéneos.
Como que la atmósfera terrestre no es homogénea, al propagarse en ella, la luz
experimenta una desviación. La dirección según la cual observamos los astros
forma con la dirección en la que deberíamos observarlos, si no existiera el
fenómeno de la refracción, un ángulo llamado refracción astronómica (ver 1.6.3).
Podemos dar
una teoría de la refracción, suficiente en la mayoría de las aplicaciones,
suponiendo:
1°) que la
densidad del aire decrece con la altitud y no depende más que de la altitud.
2°) que las
superficies de igual densidad, también superficies de igual índice de
refracción, son planos horizontales. Se desprecia la curvatura de la Tierra.
FIG
36.1
Para
simplificar el razonamiento sustituyamos esta atmósfera, cuyo índice de
refracción decrece de manera continua,
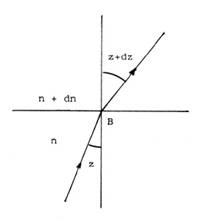
por una atmósfera formada por capas homogéneas muy delgadas, separadas
por superficies refringentes planas y horizontales. La capa índice n tiene
encima una capa de índice n+dn (siendo dn negativo) y el rayo luminoso que
procede del suelo y va a parar al punto B
de la superficie de separación, formando un ángulo de incidencia z, se refracta con un ángulo de
refracción z+dz (Fig. 36.1). Apliquemos la ley de Descartes:
![]()
La cantidad nsenz
se mantiene constante a lo largo del rayo luminoso y esta propiedad se conserva
si se aumenta indefinidamente el número de capas. Admitiremos que dicha constancia se mantiene aun con una
variación continua del índice de refracción.
FIG
37.1
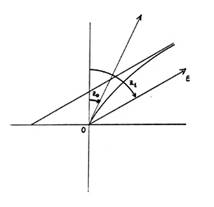
Cuando nos separamos del suelo siguiendo el rayo luminoso, n decrece y por consiguiente z aumenta: el rayo vuelve su concavidad hacia el suelo (Fig. 37.1). Supongamos que parte de un punto O en el cual el índice de refracción es no y que forma con la vertical en O un ángulo z0. El rayo se mantiene siempre en el plano vertical que contiene su tangente en O: No hay refracción en acimut. Sigamos al rayo luminoso hasta su salida de la atmósfera refringente, es decir, hasta donde la curvatura se hace despreciable y el índice de refracción del medio es la unidad. La tangente al rayo luminoso, que se confunde con su asíntota, forma entonces un ángulo z1 con la vertical en el punto O (Fig. 37.1). Se llama refracción astronómica la diferencia:
![]()
Supongamos ahora
que el rayo proviene de un astro E
cuya distancia cenital verdadera es z1.
E1 observador situado en O ve este astro en la dirección de donde le llega la luz, es decir en
la dirección de la tangente en O al rayo luminoso, siendo zo
la distancia cenital observada: la refracción astronómica acerca los astros al
cenit. Puesto que el producto nsenz es constante, tenemos:
de donde:
![]() (19.1)
(19.1)
R es lo suficientemente pequeño como para que, en primera aproximación,
se pueda confundir su seno por el arco expresado en radianes y reemplazar su
coseno por la unidad. La ecuación (19.1) es entonces:
![]()
y haciendo
![]()
también:
fórmula aproximada para z0
£ 60°.
En
condiciones normales de temperatura y presión (0°C, 76 cm de mercurio), el
índice de refracción del aire es no
= 1,00029255 para una longitud de onda de 0'',575, para la cual en general las
lentes son acromáticas. Se tiene pues, en tales condiciones:
![]()
valor de la refracción normal para z0 = 45°.
A la temperatura t y a la presión P, se tiene, admitiendo la Ley
de Gladstone:
![]()
En estas condiciones, para un
lugar de observación a la temperatura t
(en grados centígrados) y la presión P
(en centímetros de mercurio), la refracción valdrá, según (20.1):
La fórmula (21.1),
válida con buena aproximación cerca del cenit, no puede utilizarse para astros
que se hallen cerca del horizonte. Entonces no pueden despreciarse la
curvatura de la Tierra ni la de las superficies de igual índice de refracción,
ya que el rayo luminoso recorre una distancia mucho mayor por la atmósfera refrigente.
Se demuestra que el invariante
de la refracción adopta ahora la forma nrsen
z=cte., donde r es la distancia al centro de la Tierra, y que la refracción viene
dada por la fórmula de Laplace:
con bo=l0/r0, donde l0
es la latitud que tendría una atmósfera homogénea cuyo peso especifico fuera el
del aire en O y que ejerciera en O la misma presión que la atmósfera real
y r0 es el radio del
observador. Calculando los valores de los coeficientes de tan z0 y tan3 z0 de la fórmula (22.1), en condiciones normales se obtiene para R:
![]()
fórmula válida hasta alrededor de los 80° de
distancia cenital.
1.9.3 Refracción en las proximidades del
horizonte
Con una buena aproximación, la
fórmula de Laplace nos da la refracción astronómica para valores no muy grandes
de la distancia cenital, sin hacer ninguna hipótesis sobre la ley de
distribución de las densidades en la atmósfera. Si se diera a priori una tal
ley, se podría prolongar la fórmula de Laplace y obtener un desarrollo
alternado según las potencias impares de tan
z0 (que dejaría de ser convergente en el horizonte) de la forma:
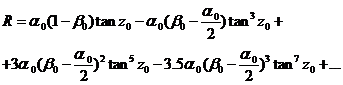 (23.1)
(23.1)
La refracción normal vendría
dada entonces por la fórmula:
![]()
Los dos primeros términos de (23.1) nos dan la fórmula de Laplace (22.1)
válida para la astronomía meridiana, pues las medidas precisas de las
distancias cenitales no se realizan más allá de los 60°.
Hay fórmulas finitas que
permiten establecer la refracción cerca del horizonte. Por ejemplo:
![]()
donde
![]()
y Y representa la función
![]()
Si en ella tomamos a0 = 60'',343 y a = 0,0011078 obtenemos, en condiciones normales:
![]()
siendo en el mismo horizonte:
![]()
La ley empírica, puesta en
evidencia con ocasión de la fórmula de Laplace, según la cual la refracción
astronómica es prácticamente independiente de la ley de densidad de la
atmósfera se verifica de una manera muy satisfactoria hasta la distancia
cenital de 85°. Es solamente a partir de observaciones realizadas de 2° ó 3°
del horizonte cuando se podrá esperar deducir la ley de densidad. Pero,
entonces, las refracciones anormales que se manifiestan con tanta frecuencia a
la salida y puesta del Sol, que deforman el disco de un modo tan aparente, restarán
mucha precisión a las mediciones.
En el Anuario de San Fernando se
da para la refracción la fórmula:
![]()
donde el factor R' = R0 (1 + Aa) se denomina refracción
corregida de temperatura y donde R0 es la refracción normal calculada para una latitud de 45°, una altitud de
cero metros, una temperatura de cero grados centígrados, una presión de 1 tor
(a 0°C) y una presión de vapor de agua de 6 mm de mercurio. Ro está tabulada en función
de la distancia cenital. Los parámetros A,
B, a, b, también tabulados, son tales que: A es función de la temperatura, B es función de la presión, a es función de la distancia cenital z0 si 45° £ z0
£ 81° y además de la temperatura si z0 ³ 81° (si z0
< 45° se toma a = 1), b
es función de R' si z0 > 60° (si z0
< 60° se toma b = 1).
1.9.4 Corrección de refracción en coordenadas
horizontales y horarias
En coordenadas horizontales la
refracción sólo modifica la altura, no el acimut. Si el índice o designa las coordenadas
observadas y el 1 las corregidas tenemos:
![]()
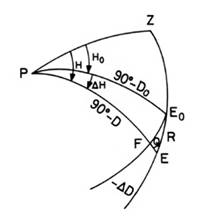
FIG 38.1
Esta situación cambia al
considerar un sistema de coordenadas horarias. Sean E la posición real de un astro y E0 la posición aparente debida a la refracción. E y E0
se encuentran sobre un mismo vertical y la diferencia de sus alturas constituye
la refracción astronómica R (Fig.38.1) . Si trazamos por E0 un paralelo celeste, y llamamos F a su intersección con el horario que pasa por E, obtenemos dos triángulos no esféricos
(un paralelo no es, en general, un círculo máximo). No obstante, al ser R pequeño, podemos considerar PFE0 como un triángulo
esférico y FEE0 como un
triángulo plano, con lo que si llamamos:
![]()
obtenemos (Fig.38.1):
![]()
y como
DD y DH son pequeños:
![]()
y también:
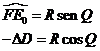
siendo Q
el ángulo paraláctico. En definitiva, pues:
![]()