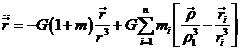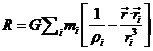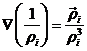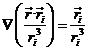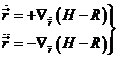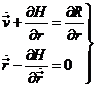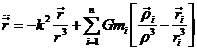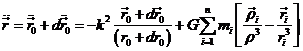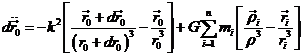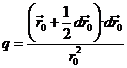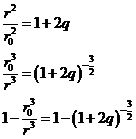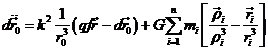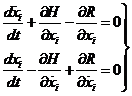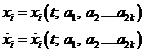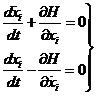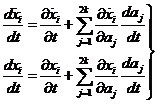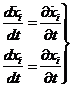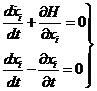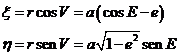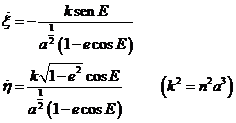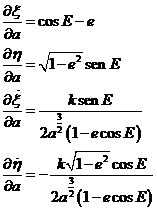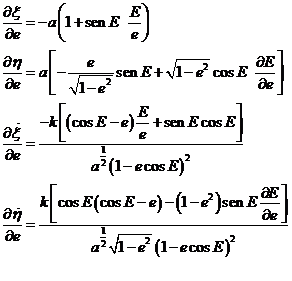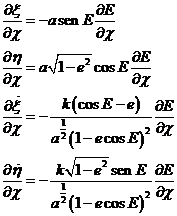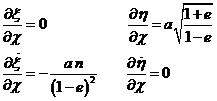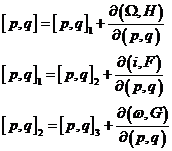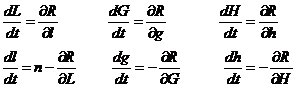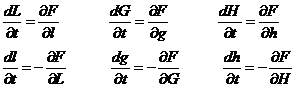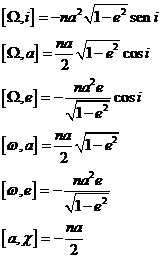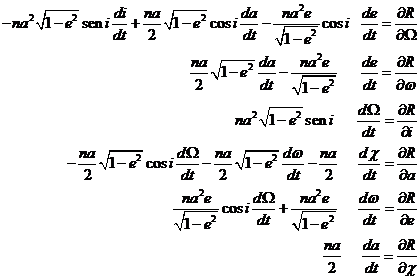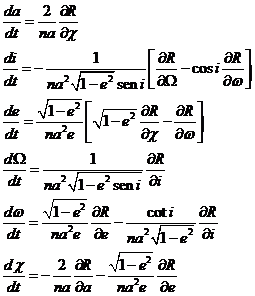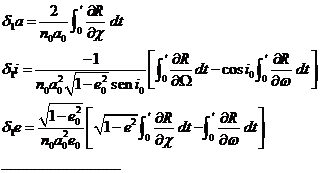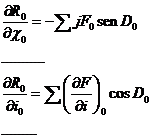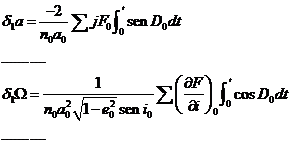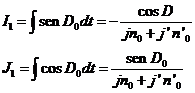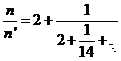8.8 Perturbaciones debidas a la acción de varios astros

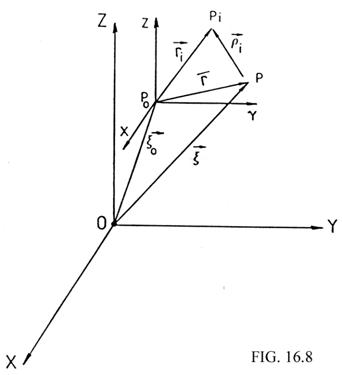
Consideremos n + 2 puntos materiales P₀, P, P_i (i = 1, 2, ...n) de masas respectivas m₀, m, m_i (i = 1, 2, ...n) y sean y los vectores de posición de P₀ y P en un sistema inercial 0; X, Y, Z (Fig.16.8). Tomemos un sistema de ejes cartesianos con origen en P₀ y ejes x, y, z paralelos a los X, Y, Z, respectivamente. Llamemos y a los vectores de posición de P y P_i con respecto a P₀ y al vector de posición de P_i con respecto a P. De acuerdo con la fórmula (32.7) de 7.4, suponiendo m₀ = 1 y refiriendo las otras masas a esta unidad, la ecuación del movimiento de P con respecto a P₀ será

(73.8)

en la que el primer término del segundo miembro representa la acción del cuerpo P₀ sobre el cuerpo de masa m, el primer término en el paréntesis la acción de los cuerpos de masas m_i sobre el de masa m y el segundo término en el paréntesis representa la acción de los cuerpos de masas m_i sobre el primario de masa m₀ = 1. Evidentemente esta fórmula (73.8) se puede aplicar tanto al estudio del movimiento de un planeta del sistema solar (P₀ = Sol) como a un satélite artificial de cualquier planeta o satélite natural.

La parte de (73.8) que depende de m_i es la aceleración perturbatriz o fuerza perturbatriz por unidad de masa y es fácil ver que deriva de una función de fuerzas

(74.8)

llamada función pertubatriz.

Podemos obtener la formulación canónica de las ecuaciones del movimiento por consideraciones análogas a las planteadas en 7.1. En efecto, observemos que se verifica

(75.8)

(76.8)

Sustituyendo (75.8) y (76.8) en (73.8) obtenemos:

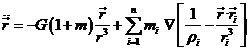(77.8)

Teniendo en cuenta (74.8) y haciendo

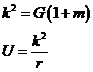
nos queda

(78.8)

Introduciendo ahora la función hamiltoniana H definida en (7.1) y operando de manera análoga a como hemos operado allí, tendremos las ecuaciones:

(79.8)

indicando por y los gradientes respecto a las variables y respectivamente. Las ecuaciones (79.8) son una generalización de las (9.7) y suelen escribirse también en la forma:

(80.8)

8.8.1 Perturbaciones especiales. Método de Encke

Veamos ahora como podemos integrar numéricamente las ecuaciones (73.8) para intervalos relativamente pequeños. Escribámoslas en la forma

(81.8)

Si las masas m_i desapareciesen brúscamente en un instante t, el movimiento sería kepleriano y obedecería a las ecuaciones

(82.8)

siendo el radio vector de P respecto a P₀ en el instante t₀.

Supongamos que podemos distinguir entre cuerpo perturbado y cuerpo no perturbado. A partir de la época t₀ uno y otro siguen trayectorias distintas; pero, tienen evidentemente las mismas posiciones y las mismas velocidades iniciales

Supongamos que hemos calculado el valor numérico de las coordenadas en función del tiempo y pongamos

De esta forma ponemos en evidencia las perturbaciones de las coordenadas, o dicho de otra forma, las coordenadas diferenciales de la posición perturbada con relación a la posición kepleriana.

Continuemos designando por m_i las masas de los astros perturbadores y por sus coordenadas. Si, como ocurre normalmente, nos proponemos determinar las perturbaciones ejercidas sobre un pequeño planeta o sobre un cometa por uno de los grandes planetas cuya teoría analítica ha sido completamente desarrollada y que no sufre ninguna perturbación sensible por parte del astro estudiado, es legítimo suponer conocidos los valores numéricos de las posiciones en función del tiempo.

Las coordenadas satisfacen la ecuación (81.8) de modo que

(83.8)

donde

Si restamos de los dos miembros de (83.8), teniendo en cuenta (82.8), obtendremos:

(84.8)

Las perturbaciones pueden determinarse por integración directa de las ecuaciones (84.8). El término puede calcularse, para alguna fase de la integración, a partir de las leyes del movimiento elíptico y el se calculará para cada fase de la integración extrapolando . Ahora bien, este proceso no es práctico, puesto que es muy pequeño y con lo cual resulta que su diferencia, primer término de , es muy poco significativa. Para salvar esta dificultad Encke ideó una transformación que dió lugar al llamado método de Encke.

Se tiene

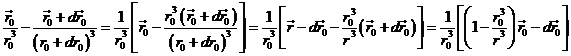
Hagamos ahora

de donde

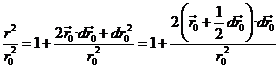
y llamemos

(85.8)

Tendremos:

(86.8)

Si es tan pequeño en comparación con que su cuadrado se puede despreciar, entonces escribiremos (85.8) en la forma:

(87.8)

función más fácil de calcular que la (85.8).

Si es q 1 podemos obtener un valor aproximado de (86.8) desarrollando en serie

(88.8)

y todavía podemos definir una función

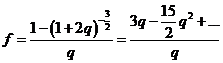
que cuando q 0 vale f = 3.

La ecuación (84.8), resulta, con estos cambios:

(89.8)

y es la que debe integrarse en el método de Encke. La solución comprende seis constantes de integración que se toman de modo que las coordenadas y las componentes de la velocidad en una órbita no perturbada (, ) sean las mismas que las de la órbita perturbada en una época particular para la cual y son nulos. La fecha en la que esto ocurre se llama la fecha de osculación.

Las ecuaciones (89.8) son rigurosas si q se calcula con la fórmula (85.8). Para iniciar la integración q se calcula con la fórmula (87.8). Las perturbaciones van siendo incrementadas gradualmente y cuando sus cuadrados ya son apreciables entonces se utiliza la fórmula (85.8).

Si limitamos la integración a una época dada t₁, obtendremos y correspondientes a dicha época. Con y podremos determinar los elementos de una nueva órbita osculatriz siendo t₁ la época origen. El proceso se puede seguir hasta conseguir que las diferencias O – C sean suficientemente pequeñas. De esta forma, la órbita perturbada se halla dividida en una serie de arcos cada uno de los cuales ha sido objeto de una operación particular. Decimos que con este proceso hemos rectificado la órbita.

El método de Encke es uno de los métodos que se conocen con el nombre genérico de método de 1as perturbaciones especiales. Se aplica al cálculo de efemérides de pequeños planetas para los cuales no se ha establecido una teoría analítica, al cálculo del movimiento de cometas perturbado por los grandes planetas, etc. Últimamente se ha recurrido al método de las perturbaciones especiales para controlar en ciertos puntos la teoría analítica de algunos planetas, principalmente Marte y Saturno.

8.8.2 Método de variación de las constantes de Lagrange

Siguiendo a Lagrange consideraremos un sistema algo más general que el (80.8) de 2k ecuaciones con 2k incógnitas que escribiremos de la forma

(90.8)

con funciones de las 2k variables y el tiempo.

Supongamos que las funciones

(91.8)

que dependen del tiempo y de las constantes a₁,..., a_2k, son las integrales del sistema

(92.8)

que resulta de (90.8) con .

El método de Lagrange consiste en suponer que las integrales del sistema (90.8) son de la forma (91.8) donde las constantes a₁, a₂, ... ,a_2k se consideran variables con el tiempo. De este modo tendremos:

(93.8)

mientras que si las a_j (j = 1, 2,..., 2k) son constantes será:

(94.8)

y por tanto, en este caso, el sistema (92.8) deberá escribirse en la forma:

(95.8)

Sustituyendo (93.8) en (90.8) teniendo en cuenta (95.8) queda:

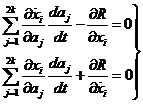(96.8)

y multiplicando la primera de estas igualdades por , la segunda por y sumando respecto al índice i obtenemos:

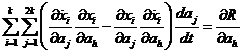(97.8)

ecuaciones de Lagrange que suelen escribirse de la forma

(98.8)

donde

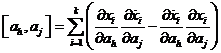(99.8)

son los llamados paréntesis de Lagrange.

Recordemos algunas propiedades de estos paréntesis que nos van a ser útiles:

a) Si a_h = a_j. el paréntesis es nulo.

b) para cualquier par de valores de a_h y a_j.

c) cualesquiera que sean a_h y a_j.

d) Un giro del sistema de referencia alrededor de uno cualquiera de los ejes de modo que O; x, y, z → O; x₁, y₁, z₁ transforma el paréntesis de Lagrange de la siguiente forma

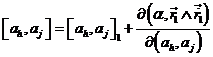
donde y son los transformados de los vectores y con este giro, α es el ángulo de giro y 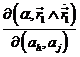es el jacobiano de la transformación.

8.8.3 Aplicación al movimiento planetario

Para aplicar el método de variación de las constantes al movimiento planetario necesitamos algunas expresiones deducidas al estudiar el movimiento elíptico (3.6) y sus derivadas con respecto al tiempo que listamos a continuación:

(100.8)

(101.8)

(102.8)

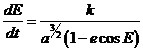(103.8)

De las (100.8) y (101.8) deducimos:

(104.8)

(105.8)

(106.8)

En virtud de la independencia del tiempo de los paréntesis de Lagrange (propiedad c)) podemos calcular el valor de estas derivadas para cualquier instante t. Así, si hacemos t = T (época de paso a por el periastro) y tenemos en cuenta que en el periastro es E = 0, de (102.8) obtenemos:

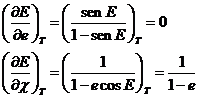(107.8)

de donde se deducen los siguientes valores en el periastro para las derivadas (104.8), (105.8) y (106.8).

(108.8)

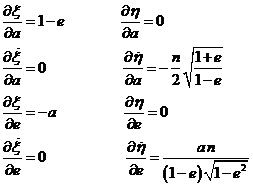
Recordemos, por otra parte, los giros que nos permiten pasar del sistema (P₀; x,y,z) al sistema de coordenadas sobre la órbita del punto P de masa m (3.11.3 y 3.12). Si llamamos p y q a dos cualesquiera de los elementos orbitales y aplicamos la propiedad de los paréntesis de Lagrange que hemos designado por d), el paréntesis [p, q], a causa de estos giros, se irá transformando en otros [p, q]₁, [p, q]₂, [p, q]₃ , dados por las expresiones:

(109.8)

siendo:

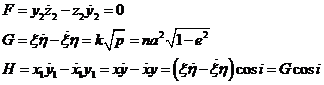
De (109.8) por sustituciones sucesivas se obtiene

(110.8)

siendo, por definición de peréntesis de Lagrange:

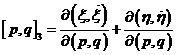
Pero, aplicando una conocida propiedad de los jacobianos y teniendo en cuenta las expresiones (108.8) podemos escribir:

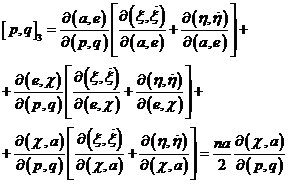
y sustituyendo en (110.8) resulta:

(111.8)

Para simplificar la expresión (111.8) se utiliza la variable

cuya derivada respecto a p es

y, por tanto,

(112.8)

El proceso de cálculo que hemos seguido para llegar a la fórmula (112.8) constituye lo que se conoce con el nombre de método de Whittaker.

Las ecuaciones de Lagrange (98.8) para un movimiento orbital perturbado se pueden obtener de manera sencilla sustituyendo los elementos a_h, a_j (o p, q) por cualquiera de los elementos orbitales. Así, cuando utilicemos las variables los paréntesis de Lagrange tomarán los valores:

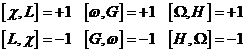(113.8)

siendo nulos todos los restantes. Luego, en este sistema de variables, las ecuaciones (98.8) se escribirán:

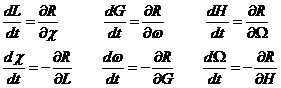(114.8)

sistema que constituye una de las formas canónicas de las ecuaciones del movimiento planetario.

Si, en lugar de las anteriores, utilizamos las variables , , , llamadas variables de Delaunay, obtendremos:

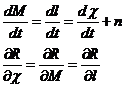
resultando el sistema

(115.8)

Si en lugar de la función perturbatriz R consideramos la función

al sustituir R en función de F en (115.8) obtendremos el sistema de ecuaciones

(116.8)

utilizado por Delaunay en su teoría de la Luna.

Si tomamos las variables ordinarias y calculamos los paréntesis de Lagrange utilizando (112.8) encontraremos que los únicos no nulos son:

(117.8)

y los que resultan de permutar las variables entre sí que en virtud de la propiedad b) tienen signos contrarios.

Sustituyendo los valores (117.8) y sus opuestos en las ecuaciones (98.8) se obtiene el sistema:

(118.8)

Despejando de (118.8) las derivadas de los elementos orbitales se obtiene:

(119.8)

sistema fundamental en el estudio del movimiento planetario que nos da las variaciones de los elementos orbitales de un determinado planeta (de masa m) a partir de un cierto instante en el que conocemos su órbita osculatriz.

Estas ecuaciones (119.8) son rigurosas y aunque las hayamos deducido para las perturbaciones producidas sobre un planeta de masa m por otros cuerpos del sistema solar (recordemos (74.8)), se pueden utilizar cuando R es debida a cualquier otra causa; por ejemplo, a la forma y distribución de la masa de un planeta cuando se aplican a un satélite artificial de dicho planeta.

Es fácil pasar del sistema (119.8) al sistema de ecuaciones de Gauss (I a VI del Cap. 8) sin más que tener en cuenta que la R a la que nos estamos refiriendo como función perturbatriz es la aceleración perturbatriz. Basta pues escribir las derivadas de R que aparecen en (119.8) en función de las componentes radial, transversal y perpendicular a la órbita.

8.8.4 Solución de las ecuaciones planetarias de Lagrange

Se puede establecer la teoría analítica general de las perturbaciones en el sistema planetario utilizando las ecuaciones (119.8) y la función R (74.8) escritas para cada uno de los planetas siendo el Sol el primario de masa 1. Sin embargo, en la solución de Lagrange la función R se escribe en la forma de d’Alambert

(120.8)

donde los coeficiente F son los productos de m_i (masa de los cuerpos perturbadores) por ciertas funciones de los ejes mayores, de las excentricidades y de las inclinaciones, es decir, si, para simplificar y como hacen la mayoría de los autores, suponemos un solo cuerpo perturbador de masa m’,

(121.8)

y donde los argumentos D dependen linealmente de las anomalías medias, de los argumentos de los nodos y de los argumentos de los perihelios de los cuerpos perturbadores y del perturbado, o sea:

(122.8)

con j, j’, k, k’, l, l’ enteros.

Como que las masas de los planetas son muy pequeñas comparadas con la del Sol, podemos suponer que la variación de los elementos dada por las ecuaciones (119.8) es muy pequeña; por consiguiente, para resolver el sistema de ecuaciones diferenciales de Lagrange podemos proceder por aproximaciones sucesivas.

Para obtener las perturbaciones de primer orden en la primera aproximación reemplazaremos en los segundos miembros todos los elementos por sus valores iniciales (elementos osculadores) a₀, e₀, i₀, ... e integraremos después con relación al tiempo. Tendremos:

(123.8)

Teniendo en cuenta (120.8):

(124.8)

y sustituyendo en (123.8):

(125.8)

En estas seis ecuaciones (125.8) intervienen integrales de dos tipos:

cuando el tiempo figura linealmente en los argumentos D₀, y

cuando y, por tanto, el tiempo no figura en la expresión de D₀.

En el primer caso las integrales dan las desigualdades periódicas de los elementos y en el segundo caso dan las perturbaciones seculares.

Observamos que en el segundo supuesto (), en virtud de las expresiones (124.8), en las perturbaciones de primer orden y en la primera aproximación las perturbaciones del eje mayor y las del movimiento medio no contienen términos seculares.

Generalmente, los valores j y son tales que no es una cantidad particularmente pequeña en comparación con y los periodos de los términos en que figuran son del mismo orden que los periodos orbitales de los dos cuerpos implicados. Estos términos reciben el nombre de desigualdades de corto periodo. Si j y j’ son tales que hacen que tome un valor, sinó nulo, muy pequeño sin ser nulos j y j’, entonces existirá una relación aproximada de conmensurabilidad entre el movimiento medio del cuerpo perturbado y el del perturbador. Las desigualdades correspondientes tienen un periodo muy largo y reciben el nombre de desigualdades de 1argo periodo; además, su coeficiente, que contiene el factor puede tomar un valor muy grande independientemente de que F₀ sea grande o pequeño. Se dice entonces que es un pequeño divisor.

El ejemplo más notable de desigualdades a largo periodo es dado por Júpiter y Saturno cuyos movimientos medios son respectivamente

Si desarrollamos la razón , en fracción contínua obtenemos:

Las fracciones reducidas son:

y la que da el divisor más pequeño es . Luego:

El periodo de esta desigualdad abarca 883 años; la longitud media de Júpiter puede ser perturbada de unos y la de Saturno de unos . Estas son las desigualdades más importantes debidas a las perturbaciones en el sistema solar.

ANTERIOR

ÍNDICE

CAPITULO 9