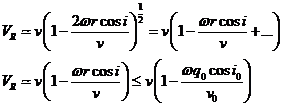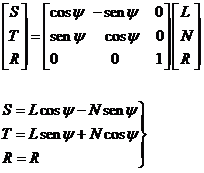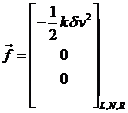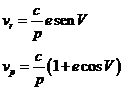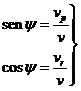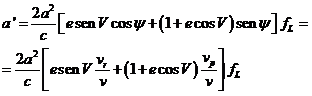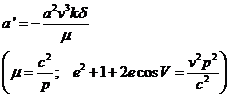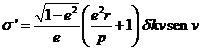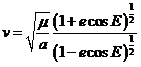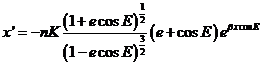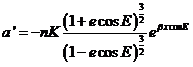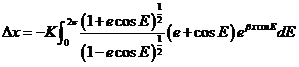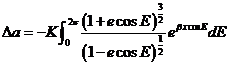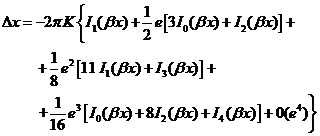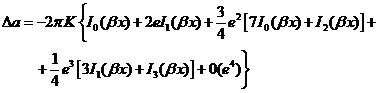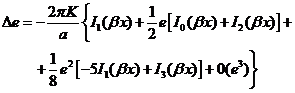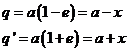8.5 Perturbaciones debidas a la resistencia de la atmósfera
Para el estudio de las perturbaciones
debidas al efecto de la atmósfera se hacen diversas hipótesis simplificativas:
a) Se supone la Tierra esférica
b) La densidad de la atmósfera decrece exponencialmente con la altura
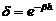
c) La densidad del aire no varía con el tiempo (se desprecian las
mareas: la Luna y el Sol producen mareas sobre la atmósfera, llegando a variar
la densidad hasta un 20% por este efecto)
d) La resistencia de la atmósfera al movimiento de un
cuerpo es proporcional al cuadrado de la velocidad del cuerpo
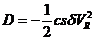 (26.8)
(26.8)
donde c = coeficiente de resistencia ( 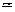 2,2)
2,2)
s = área de la sección recta
del satélite
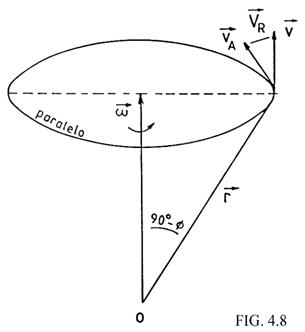
e) La atmósfera gira con la Tierra; es decir, el punto r
describe un paralelo (Fig. 4.8). Si 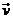 es la velocidad
del satélite,
es la velocidad
del satélite, 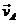 la velocidad de la
atmósfera y
la velocidad de la
atmósfera y 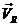 la velocidad
resultante, tenemos:
la velocidad
resultante, tenemos:
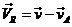
siendo
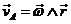
o también
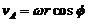 (27.8)
(27.8)
donde ω
es la velocidad angular de la
Tierra y 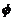 la latitud del punto r.
la latitud del punto r.
Si llamamos γ al ángulo que forman 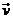 y
y 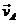 , podemos escribir:
, podemos escribir:
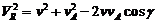
El ángulo
entre 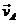 y
y 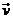 no diferirá
mucho del que formen
no diferirá
mucho del que formen 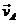 con la proyección
con la proyección 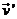 de
de 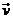 sobre la
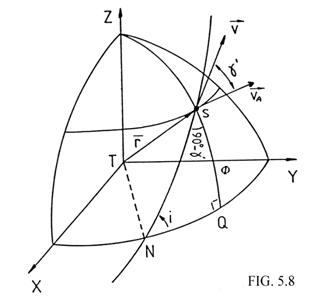
tangente a la órbita (Fig. 5.8), de modo que si es
sobre la
tangente a la órbita (Fig. 5.8), de modo que si es 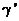 , tendremos:
, tendremos:
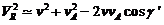
y teniendo
en cuenta que en el triángulo NSQ de la (Fig. 5.8) se
verifica
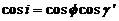
recordando
la fórmula (27.8), podemos escribir:
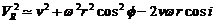
El término 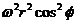 es pequeño. En un
punto ecuatorial es del orden de 0.5 km/s. A 300 km de altitud es del orden de
8 km/s. Luego, podemos escribir:
es pequeño. En un
punto ecuatorial es del orden de 0.5 km/s. A 300 km de altitud es del orden de
8 km/s. Luego, podemos escribir:
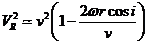
es decir:
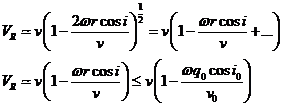
siendo q0 la distancia al
perigeo inicial
v0 la velocidad del satélite al pasar
por el perigeo inicial
i0 inclinación del satélite al
pasar por el perigeo inicial
En general 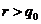 y
y 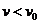 , por tanto
, por tanto 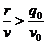 y
y 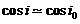 pero el cociente está restando
de la unidad, de ahí la desigualdad dada.
pero el cociente está restando
de la unidad, de ahí la desigualdad dada.
Vemos pues que VR está acotada por v y
por un factor de reducción
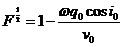
El cuadrado de este factor F es tal que está
comprendido entre 1 y 0.9
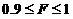
Con esto
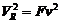
y recordando
(26.8) podemos escribir:
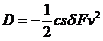 (28.8)
(28.8)
y teniendo en cuenta que si 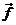 es la fuerza perturbatriz por unidad de masa,
será
es la fuerza perturbatriz por unidad de masa,
será
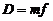 (29.8)
(29.8)
haciendo 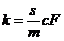 e igualando (28.8)
y (29.8), obtendremos
e igualando (28.8)
y (29.8), obtendremos
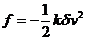 (30.8)
(30.8)
y de (30.8),
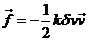 (31.8)
(31.8)
Para el cálculo de las perturbaciones debidas a la atmósfera
trabajaremos en la base L, N, R, definida de la siguiente
forma:
L dirigido según la tangente a la órbita en la
posición del satélite
N dirigido según la normal
R perpendicular al plano de la
órbita
Expresaremos las ecuaciones de Gauss en esta nueva base. El cambio se
expresará por
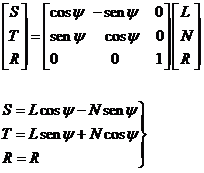 (32.8)
(32.8)
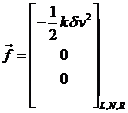 (33.8)
(33.8)
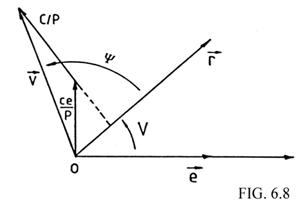 En cuanto a la velocidad recordemos que en el sistema S,T,R
es:
En cuanto a la velocidad recordemos que en el sistema S,T,R
es:
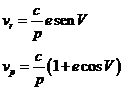
de
aquí que, según la Fig.6.8:
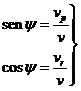 (34.8)
(34.8)
Las dos primeras ecuaciones de Gauss se mantendrán ya que el tercer eje
de uno y otro sistema coinciden. Es decir, volvemos a encontrar (I) y (II). Para hallar las
restantes tendremos en cuenta los cambios indicados.
Así, para calcular a partiremos de (III) y
escribiremos, sustituyendo fS y fT por sus
correspondientes valores deducidos de (32.8) y (34.8), teniendo además en cuenta que
partiremos de (III) y
escribiremos, sustituyendo fS y fT por sus
correspondientes valores deducidos de (32.8) y (34.8), teniendo además en cuenta que 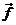 sólo tiene primera componente,
sólo tiene primera componente,
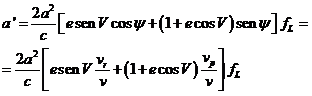
y teniendo
en cuenta los valores de vr,
vp y fL
(primera componente de 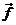 ) queda
) queda
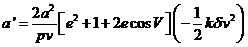
o
lo que es lo mismo:
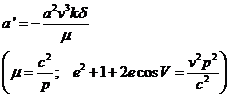 (35.8)
(35.8)
Análogamente, para calcular e’ partiremos de (IV) y aplicando los mismos cambios y recordando que 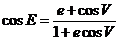 obtendremos:
obtendremos:
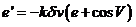 (36.8)
(36.8)
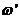 y
y 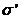 se obtendrán a partir
de (V) y (VI). Serán:
se obtendrán a partir
de (V) y (VI). Serán:
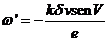 (37.8)
(37.8)
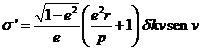 (38.8)
(38.8)
La presencia del término sen V en las ecuaciones (37.8) y (38.8) hará que al integrarlas
obtengamos
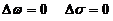 (39.8)
(39.8)
Deberemos pues preocuparnos sólamente de a’ y e’.
En las fórmulas (35.8)
y (36.8) intervienen la densidad 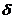 y la velocidad v
que podemos expresar en función de la anomalía excéntrica E. En efecto,
recordemos que
y la velocidad v
que podemos expresar en función de la anomalía excéntrica E. En efecto,
recordemos que 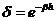 (39.8)
y escribámosla para el perigeo. Si llamamos
(39.8)
y escribámosla para el perigeo. Si llamamos 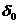 a la densidad en dicho
punto tendremos:
a la densidad en dicho
punto tendremos:
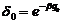 (40.8)
(40.8)
y tomando h
= r y dividiendo (39.8) por (40.8):
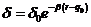
donde
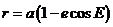 .
.
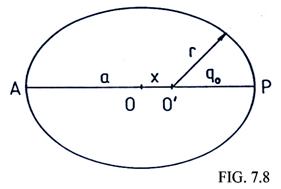
Por otra
parte, llamemos x a
la semidistancia focal (Fig.7.8) :
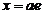
con lo cual
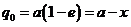
y
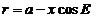
Por tanto
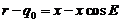
y
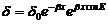 (41.8)
(41.8)
Para la velocidad escribiremos:
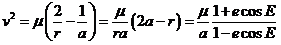
de donde
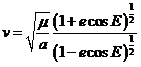 (42.8)
(42.8)
Para simplificar aun más calcularemos x’ y trabajaremos con a’
y x’ en lugar de hacerlo con a’ y e’.
Escribiremos:
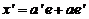
y teniendo
en cuenta (35.8) y (36.8)
obtendremos:
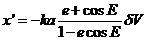
pero,
sustituyendo 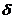 y v por
(41.8) y (42.8), finalmente:
y v por
(41.8) y (42.8), finalmente:
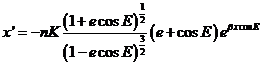 (43.8)
(43.8)
donde
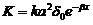
Análogamente, sustituyendo en (35.8) 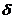 y
y 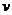 por (41.8) y (42.8), se obtiene:
por (41.8) y (42.8), se obtiene:
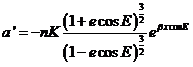 (44.8)
(44.8)
De (43.8) obtendremos
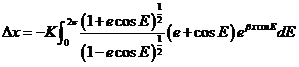 (45.8)
(45.8)
y de (44.8):
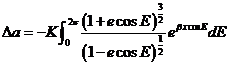 (46.8)
(46.8)
Al resolver las integrales (45.8)
y (46.8) se obtiene:
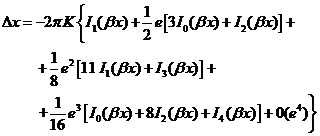 (47.8)
(47.8)
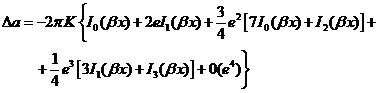 (48.8)
(48.8)
De 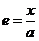 , tomando incrementos se obtiene
, tomando incrementos se obtiene
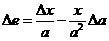
y
sustituyendo 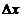 y
y 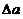 por sus valores (47.8) y (48.8):
por sus valores (47.8) y (48.8):
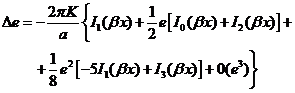 (49.8)
(49.8)
Tanto en 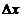 como en
como en 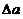 y
y 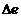 ,
, 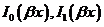 ,… representan las funciones de Bessel
,… representan las funciones de Bessel
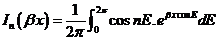
Si designamos por q y q’ las distancias perihélica y
afélica respectivamente, tendremos:
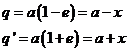
y de (47.8) y (48.8):
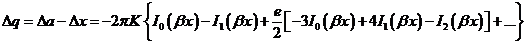
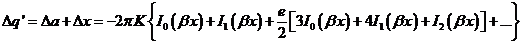
En primera aproximación se puede suponer 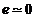 y al comparar los incrementos de
q y q’, obtendremos:
y al comparar los incrementos de
q y q’, obtendremos:
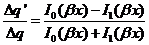
Si se toma 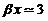 y e < 0.2, valores
normales en el lanzamiento de satélites, este cociente es:
y e < 0.2, valores
normales en el lanzamiento de satélites, este cociente es:
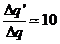
lo cual nos
dice que el apogeo baja una diez veces más deprisa que el perigeo. La órbita
tiende a hacerse circular.
Como que a disminuye, en media el satélite
describe una espiral y acaba quemándose en la atmósfera. Es la “muerte” de un
satélite artificial en órbita alrededor de la Tierra.
![]()
![]() 2,2)
2,2) ![]() es la velocidad
del satélite,
es la velocidad
del satélite, ![]() la velocidad de la
atmósfera y
la velocidad de la
atmósfera y ![]() la velocidad
resultante, tenemos:
la velocidad
resultante, tenemos: ![]()
![]()
![]() la latitud del punto r.
la latitud del punto r.![]() y
y ![]() , podemos escribir:
, podemos escribir:![]()
![]() y
y ![]() no diferirá
mucho del que formen
no diferirá
mucho del que formen ![]() con la proyección
con la proyección ![]() de
de ![]() sobre la
tangente a la órbita (Fig. 5.8), de modo que si es
sobre la
tangente a la órbita (Fig. 5.8), de modo que si es ![]() , tendremos:
, tendremos:![]()
![]()
![]()
![]() es pequeño. En un
punto ecuatorial es del orden de 0.5 km/s. A 300 km de altitud es del orden de
8 km/s. Luego, podemos escribir:
es pequeño. En un
punto ecuatorial es del orden de 0.5 km/s. A 300 km de altitud es del orden de
8 km/s. Luego, podemos escribir:![]()