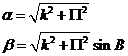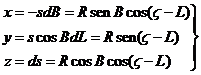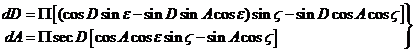4.3 Paralaje ánua
Debido al movimiento de traslación de la Tierra
alrededor del Sol, por un efecto paraláctico, las estrellas próximas parecen
oscilar alrededor de sus posiciones medias en el transcurso del año. Este
fenómeno, llamado paralaje ánua de las
estrellas, es mucho menos notable que el de la aberración ánua, pues, dada la
distancia a que se encuentran, su semiamplitud no alcanza nunca 1’’, frente a
los 20’’,5 de la aberración ánua.
FIG. 9.4
Supongamos, para simplificar el razonamiento, que
la órbita de la Tierra es circular. Sea S
el Sol y a el radio orbital (Fig.9.4). Sea E la posición de una estrella a la
distancia s del Sol, distancia que
supondremos constante, T la posición
de la Tierra en una determinada fecha y T1
la posición de la misma seis meses después. El segmento TT1 es la base de referencia para determinar la
distancia de la estrella al Sol.
Tracemos por T
una paralela TE1 a SE y designemos por q y q1 los ángulos E1TS y ETS.
Del triángulo STE en el cual el
ángulo SET es q-q1, deducimos:
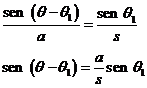
Por definición, a/s =senP donde P recibe el nombre de paralaje estelar o paralaje
ánua. Por la forma como se ha definido, P es siempre muy pequeño (menos de 1’’ ) y
se puede escribir
donde q-q1 y P están medidos en las mismas unidades
y q1 se
ha sustituido por q en el segundo miembro.
Por otra parte, también en virtud de la
definición, P representa el ángulo bajo el cual se ve desde la
estrella el radio de la órbita de la Tierra.
En la Fig. 9.4 SE
es la dirección en la que se observa la estrella desde el Sol (dirección
heliocéntrica) y TE es la dirección
en que se ve desde la Tierra en la época dada (dirección geocéntrica). Si la
estrella estuviera a distancia infinita se vería desde la Tierra en la
dirección TE1 paralela a SE. Pues bien, vemos que la dirección
geocéntrica TE está desplazada de la dirección heliocéntrica TE1 hacia la
dirección TS del Sol y que este
desplazamiento tiene lugar en el plano STE
(Sol-Tierra-estrella).
Dicho desplazamiento angular q-q1 se puede considerar como un
desplazamiento lineal de vector
que resulta más útil para la teoría que vamos a desarrollar.
Si expresamos el movimiento de la Tierra en función
del aparente del Sol, en el triángulo TSE
se tiene:
siendo 
el vector de
posición geocéntrico del Sol. Por lo que hemos dicho, esta fórmula suministra
la corrección de paralaje 
que hemos de
aplicar para pasar de coordenadas heliocéntricas 
(verdaderas) a
geocéntricas 
(aparentes).
Tomemos ahora un sistema de coordenadas X, Y,
Z con origen en el centro de la
Tierra, eje X en la dirección de
Aries, eje Y en la eclíptica, en sentido
directo, eje Z en la dirección del
polo de la eclíptica (Fig. 10.4). Tendremos para :
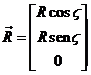
donde V representa la longitud del Sol.
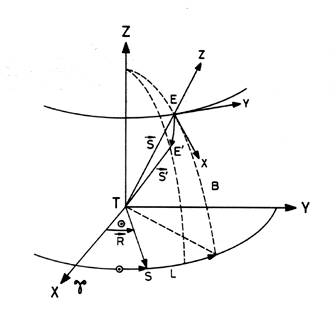
FIG. 10.4
Supongamos una estrella E cuyas coordenadas esféricas eclípticas sean L y B y sean y sus posiciones
heliocéntrica y geocéntrica respectivamente. Supongamos que podemos expresar la
posición aparente de la estrella con respecto a la posición verdadera con el
empleo de coordenadas diferenciales. Para ello tomemos con origen en la
estrella (posición verdadera expresada por la dirección desde T) unos ejes de coordenadas
rectangulares de la siguiente forma: el eje x
según el máximo de longitud que pasa por ella, en el sentido de las latitudes
decrecientes; el eje y tangente al menor de latitud en el sentido de las
longitudes crecientes, y el eje z en la dirección de . Las coordenadas de E'
(posición aparente) con relación a E,
serán:
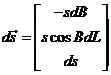
que podremos identificar con las del vector expresado en el
mismo sistema. Para ello verificaremos un giro de ángulo L alrededor de z, que
vendrá definido por la matriz R3(L) y, a continuación un giro de ángulo
(90º- B) alrededor del eje y obtenido
después del primer giro, definido por la matriz R2(90º -B).
Tendremos, por tanto:
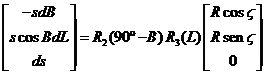
y operando y simplificando:
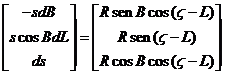
es decir:
(21.4)
donde 
es la paralaje de la estrella.
Para interpretar geométricamente las ecuaciones (21.4) escribamos, en el mismo sistema de coordenadas con
origen en la estrella E que hemos
considerado,
(22.4)
que son las ecuaciones paramétricas de una circunferencia intersección de
la esfera
x2 +y2
+z2 =R2
de radio R y centro en E con el plano
x cos B-
z sen B = 0
paralelo a la eclíptica.
Luego, como suponemos R constante, debido a la paralaje ánua, la estrella parece
describir en un año, alrededor de su posición verdadera y con movimiento
uniforme, una circunferencia de radio R
paralela a la eclíptica. Dicha circunferencia se proyecta sobre el plano xy, tangente a la esfera celeste según
una elipse de semiejes RsenB y R
y excentricidad e = cos B, llamada elipse de paralaje.
Para un observador terrestre, los semiejes mayor y
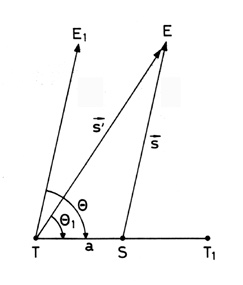
menor de la elipse subtendrán un ángulo a y b respectivamente, cuyo valor es:
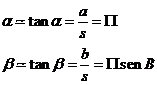
Con b ≤ a <1”.
4.3.1 Corrección de paralaje
ánua a las coordenadas ecuatoriales.
En coordenadas ecuatoriales se tendrá, pasando
antes las eclípticas geocéntricas del Sol a ecuatoriales mediante la rotación R1(-e) y aplicando después las fórmulas
diferenciales de paso de rectilíneas a esféricas:
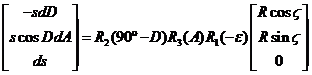
y operando e introduciendo la paralaje P de la estrella, limitándonos a la
consideración de las dos primeras componentes:
(23.4)
En las "Efemérides Astronómicas" todavía
se da otra forma a las ecuaciones (23.4), expresándolas
en función de las coordenadas rectangulares geocéntricas del Sol X,Y,Z, calculables mediante (3.4). La órbita aparente del Sol se supone ahora
elíptica y con foco en la Tierra (y no en el centro de gravedad del sistema
Tierra-Luna), y tomando como unidad la distancia media de la Tierra al Sol la
paralaje de la estrella vale, exactamente, P = l/s.
Aplicando las fórmulas de paso se tiene:
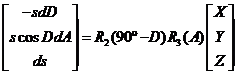
y operando y haciendo l/s = P finalmente:
(24.4)
y siendo con mucha aproximación Z=Ytane las fórmulas (24.4) suelen
escribirse, teniendo en cuenta las relaciones (18.4):
(25.4)
4.3.2 Efecto combinado de la aberración y la paralaje ánuas
En los desarrollos hasta ahora efectuados, la
aberración y la paralaje ánuas se encuentran expresadas por componentes en una
misma base x,y,z, situada en el plano
tangente a la esfera celeste en el astro y definida según coordenadas
eclípticas.
Por otra parte, la aberración y la paralaje son
fenómenos independientes, por lo que su composición será, simplemente, la suma
de (14.4) y (22.4):
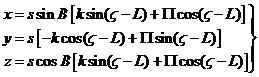
que efectuando el cambio:
k = m cos
M
P= m
sen M
puede expresarse:
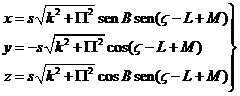
donde x,y,z, son funciones
periódicas de periodicidad un año (debido a V) y representan las ecuaciones para métricas de
una circunferencia de radio 
paralela a la eclíptica. La proyección ortogonal
sobre el plano tangente nos dará la trayectoria aparente de la estrella
alrededor de su posición verdadera, recorrida en un año, que será una elipse
de:
semieje mayor
dirgido
según y
semieje
menor 
dirigido según x
excentricidad 
y angularmente:
